ソフトウエア入門演習
オンラインテキスト目次
ビット列が与えられたとき、2 の補数表現とは、ビット列の各桁の 0 と 1 を入れ換えた後、最下位ビットに 1を加えたものである。
例えば [0110] の2 の補数は、まず 0 と 1 を入れ替えて [1001] を得、最下位ビットに 1 を加えてて桁上がりすることによって[1010] となることがわかる。 また、 [001011000] の補数表現は [110101000] である。
さて、数を表すとき普通は、当然、正負の符号も考える必要がある。 以下に見るように、正負の数をビット列で表すために2の補数表現を使う。 いま、次のような n 桁 のビット列[an-1, an-2, ...... ,a1, a0]
において、最左端の最上位ビット an-1（= 0 または 1 ） を符号ビットとして、これに次のように数
a= - an-12n +
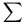k=0n-2 ak 2k
[an-2, an-3, .... , a1, a0]
に対しては、符号ビットとして 0 をつけて、n 桁ビット[0, an-2, an-3, .... , a1, a0]
で表せばよい。一方、負の整数 -b (b > 0) のときには、その絶対値 |-b|=b の(n-1) 桁ビット表示
|-b| = b = [0, bn-2, .... , b0]
に対する 2の補数表現2n - b = [1, 1 - bn-2, 1 - bn-3, .... ,1 - b1, 1-b0 + 1]
によって負整数 -b の n桁ビット表示が与えられる（2nは (n-1) 桁ビットで表すことができないために消滅したと考える）。 つまり負の数 ( -b, b > 0 )の n 桁ビット表示は、 2n-1 - b 、つまり 2n-1 からその数の絶対値 ( b )を引いた数を (n-1) 桁ビットで表示し、さらに最左端に符号化ビット 1 を付加たものに等しい。例えば、8ビット（1バイト）からなる [11111111] を調べよう。 これは、先頭の符号化ビットを 0 にした [01111111] に対応する正の数
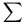k=06 2k = 127
[11111111] = -27 +
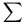k=06 2k = -128 + 127
8 ビットを使って符号付きの整数を補数表示で表現するとすれば、[10000000] = -27 = -128 から [01111111] = 127 までの全ての整数を表現することができる。
一般に、全体がn ビットで表される符号付き整数 N の数の範囲は,
-2n-1 <= N <= + 2n-1 -1
である。 実際、たとえば2バイト型（16 ビット）の整数（Javaでは short 型）では補数表現として 16 ビット長で表される整数だけを、4バイト型（32ビット）の整数（Javaでは int 型）は補数表現として 32 ビット長で表される整数だけを表すことができる。 つまり、それぞれ表せる整数の範囲は以下のようになる：となる。 例えば 2バイト型整数では
[ 0000000000000000 ] = 0
[ 0000000000000001 ] = 1
[ 0000000000000010 ] = 2
[ 0000000000000011 ] = 3
[ 0000000000000100 ] = 4
[ 0000000000000101 ] = 5
[ 0000000000000110 ] = 6
...........................
............
...........................
[ 0111111111111110 ] = 32766
[ 0111111111111111 ] = 32767
のように整数が表わされる。
もし最後の整数 32767 に 1 が加えらたとすれば、そのビット表現は
[ 1000000000000000 ]
となり、これは補数表示では数 -32768 = - 215 と表示されてしまう。
入力した整数のビット列を表示する次のように動作するプログラムを作成しよう。
% java BitTest 45 入力した整数 = 45 のビット表現 Integer.toBinaryString() = 101101 % java BitTest -45 入力した整数 = -45 のビット表現 Integer.toBinaryString() = 11111111111111111111111111010011 |
┏━━━━━━━━━ BitTest.java ━━━━━━
/*
BitTest.java
入力した整数のビット操作
usage:
> java BitTest -45↓
入力した整数 = -45 のビット表現
Integer.toBinaryString() = 11111111111111111111111111010011
*/
public class BitTest {
public static void main(String[] args) {
int n = Integer.parseInt(args[0]); // 文字列扱いの最初の引数を整数に変換
System.out.println("入力した整数 = " + n + " のビット表現");
System.out.println("Integer.toBinaryString() = " + Integer.toBinaryString(n));
}
}
┗━━━━━━━━━━━━━━━━━━━━━━━━
Javaで使えるビット演算子とシフト演算子には次がある：
|
|
ここではビットシフトの様子を理解する。 とくに符号付右シフトと符号なし右シフトの差異を理解することが大切である。
% java BitRepresentation0 整数↓ |
┏━━━━━━━━━ BitRepresentation0.java ━━━━━━/* BitRepresentation0.java 入力した整数のビット操作 usage: java BitRepresentation0 整数↓ */ public class BitRepresentation0 { public static void main(String[] args) { int n = Integer.parseInt(args[0]); // すべて文字列扱いの引数を数に変換 int i; System.out.println("入力した整数 = " + n + " のビット表現"); System.out.println("Integer.toBinaryString() = " + Integer.toBinaryString(n)); System.out.print("\n"); for(i = 0; i < 5; i++){ System.out.println("n << " + i + " = "+ Integer.toBinaryString(n << i) + ": " + (n << i)); } System.out.print("\n"); for(i = 0; i < 5; i++){ System.out.println("n >> " + i + " = "+ Integer.toBinaryString(n >> i) + ": " + (n >> i)); } System.out.print("\n"); for(i = 0; i < 5; i++){ System.out.println("n >>> " + i + " = "+ Integer.toBinaryString(n >>> i) + ": " + (n >>> i)); } } }┗━━━━━━━━━━━━━━━━━━━━━━━━
% java BitRepresentation1 整数1 整数2↓ |
┏━━━━━━━━━ BitRepresentation1.java ━━━━━━/* BitRepresentation1.java 入力した2つ整数のビット操作 usage: java BitRepresentation1 整数1 整数2↓ */ public class BitRepresentation1 { public static void main(String[] args) { int n1 = Integer.parseInt(args[0]); int n2 = Integer.parseInt(args[1]); System.out.println("整数 n1 = " + n1 + " のビット表現: "+ Integer.toBinaryString(n1)); System.out.println("整数 n2 = " + n2 + " のビット表現: "+ Integer.toBinaryString(n2)); System.out.println("n1 & n2 = " + Integer.toBinaryString(n1 & n2)); System.out.println("n1 | n2 = " + Integer.toBinaryString(n1 | n2)); System.out.println("n1 ^ n2 = " + Integer.toBinaryString(n1 ^ n2)); System.out.println("~n1 = " + Integer.toBinaryString(~n1)); System.out.println("~n2 = " + Integer.toBinaryString(~n2)); System.out.println("~n1 & n2 = " + Integer.toBinaryString(~n1 & n2)); System.out.println("n1 | ~n2 = " + Integer.toBinaryString(n1 | ~n2)); } }┗━━━━━━━━━━━━━━━━━━━━━━━━
n1 & n2 | n1 と (n1 & n2) | n1 および n1 & (n2 | n1)
の計算結果を実行するプログラムを書いて、演算子の優先順序について検討せよ。 このように、計算の表現が曖昧になるおそれがある場合には、躊躇せずにカッコをつけて計算意図を明確にすることが非常に大切である。Integer.toBinaryString(5) ---> 101
のようにしか出力しないが、実際には整数 5 は8バイト（32ビット）幅で5 ---> 00000000000000000000000000000101
のように表されているはずである。 整数のビット表をこのように32ビット幅で表示するプログラムを次のように段階的に考えよう。
1 << 31 ---> 10000000000000000000000000000000
となるはずである（これを整数の補数表示として考えれば、Java整数で表される最小の整数となる）。 これをsh31 = 1 << 31;
のように整数変数 sh31 に格納しておく。(x & sh31) >>> 31);
すればよい。System.out.print( ( (n << i ) & sh31 ) >>> 31 );
とすればよい。カッコの使い方に十分注意すること。
for (i = 0; i < 32; i++) {
System.out.print(((n << i) & sh31) >>> 31));
}
% java BitRepresentation2 整数↓ |
ソフトウエア入門演習
オンラインテキスト目次