参考：教科書 pp.139-168

データ構造とアルゴリズム入門

アルゴリズムとは、プログラムで特定の問題を解くための方法である。例えば、いくつかのデータをある順番(大きい順、小さい順)に並べるソートには、バブルソートや基本挿入法、ヒープソート、クイックソートなど数多くのアルゴリズムが考案されている。

プログラムを作成する場合に、このような既に考案されたアルゴリズムが使える場合が多く、アルゴリズムを学ぶことは、プログラミングにおいて非常に重要であると言える。

アルゴリズムで特に特徴的なことは、一般にアルゴリズムはプログラミング言語に依存しないということである。一度あるアルゴリズムを理解すれば、将来他のプログラミング言語を勉強する際にも、そのアルゴリズムが使える。アルゴリズムを知っておくと、「単にプログラムが書ける人」に対して大きく優位にたつことができる。ぜひマスターして欲しい。

またデータに特定の構造を持たせることが多い。よく使われるデータ構造には、リスト、木、スタック、キュー、グラフなどがあり、例えばグラフ用のアルゴリズム、リスト用のアルゴリズムなど、データ構造によって色々なアルゴリズムが存在する。データ構造の例として、ここではスタックとキューに触れる。

ソートのアルゴリズム

ここでは、ソート(並びかえ)のアルゴリズムとして、バブルソートとクイックソートを紹介する。

バブルソート

参考：教科書 p.143

バブルソートは以下の図の要領でソートを行う。

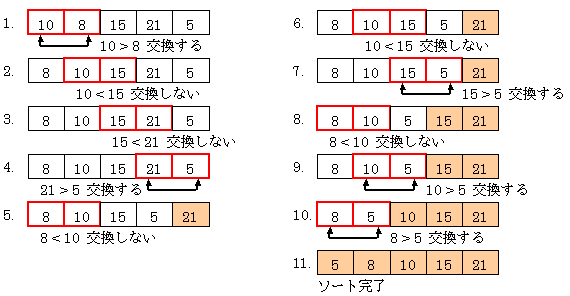
バブルソートでは、隣り合ったデータを比較し、その大小関係がおかしい場合は、データを交換する。それを順にずらしながら行っていくと、最終的にソートがされる。上の図は、小さい順(昇順)に並べる例である。ちなみに大きい順に並んだものを降順という。昇順に並べる場合、左側のデータは右側のデータより小さい値にしなければならない。まず最初は１つめのデータ(10)と２つめのデータ(8)を比べる。左側のデータのほうが大きいので大小関係がおかしい。そこで10と8を交換する。

次に１つ右側に寄って２つめのデータ(10)と３つめのデータ(15)を比べる。大小関係は正しいので交換しない。このように徐々に右にずらしていく。これを一番右まで行う(図の左下端)とデータのうち最大の値(21)が一番右に来る。このように最大の値が一番右に移動するのである。

以上のことをまた繰り返す。ただし、最大の値(21)は既に一番右に移動したので、その場所は確定した。したがって、今回は３つめと４つめのデータ比較まで行えば良い。これを行うと、２番目に大きな値(15)が右から２番目の場所に移動している。これで21と15の２つのデータの場所が確定した。

今度はデータの比較を２つめと３つめまで行えば良い。これで３番目に大きな値(10)が右から３番目の場所に移動し確定した。最後に１つめと２つめのデータを比較し交換したら全ての場所が確定し、ソートが完了する。

このように最大の値が徐々に右に寄っていく様子が泡が上っているようであるため、バブルソートと呼ばれている。バブルソートは簡単なアルゴリズムであるが、他の多くのアルゴリズムと比べ、処理時間が長くかかるのが弱点である。

課題1

以下のプログラムを元にバブルソートのプログラムを完成させよ。

public class BubbleSortTest {
    static void bubble_sort(int[] d) {
        for (int i = d.length-1; i > 0; i-- ) {
            for (int j = 0; j < i; j++) {
                System.out.println("i=" + i + ",j=" + j);
                // この部分を修正する
            }
        }
    }
    // 配列内のデータ列を表示する
    static void print_data(int[] d) {
        for(int i = 0; i < d.length; i++) System.out.print(d[i] + " ");
        System.out.println();
    }
    public static void main(String[] args) {
        int[] data = {5, 10, 3, 7, 8, 1, 9};
        print_data(data);
        bubble_sort(data);
        print_data(data);
    }
}

クイックソート

参考：教科書 pp.152-153

ここで通常の条件の中では一番高速であると言われているクイックソートを紹介する。

クイックソートの基本的考え方は、「データ列を分割して、分割された中がソートされていれば、全体もソートされることになる」ということである。このように問題を細かな問題に分割していき、細かな問題を解き、最終的にまとめて問題を解決する手法を分割統治法という。優れたアルゴリズムは分割統治法を使っているものが多い。

クイックソートで、データ列を分割する場所のデータをピボット(軸)という。ピボットはデータ列の真中にするのが普通である。分割をする場合に、ピボットより左にあるデータ列は、ピボットより右にあるデータ列よりも必ず小さな値になっていなければならない。これを行うには、データ列の左端と右端からそれぞれの値を比べ、大小関係がおかしければ交換を行う。

分割の準備ができれば、分割した細かくなった部分について同様にクイックソートを行う。つまりクイックソートは再帰的なアルゴリズムなのである。詳しくは教科書p.152を参照のこと。

クイックソートのプログラム例を以下に示す。

public class QuickSortTest {
    // 配列dのleftからrightまでの間のデータ列をクイックソートする
    static void quick_sort(int[] d, int left, int right) {
        if (left>=right) {
            return;
        }
        int p = d[(left+right)/2];
        int l = left, r = right, tmp;
        while(l<=r) {
            while(d[l] < p) { l++; }
            while(d[r] > p) { r--; }
            if (l<=r) {
                tmp = d[l]; d[l] = d[r]; d[r] = tmp;
                l++; r--;
            }
        }
        quick_sort(d, left, r);  // ピボットより左側をクイックソート
        quick_sort(d, l, right); // ピボットより右側をクイックソート
    }
    // 配列内のデータ列を表示する
    static void print_data(int[] d) {
        for(int i = 0; i < d.length; i++) System.out.print(d[i] + " ");
        System.out.println();
    }
    public static void main(String[] args) {
        int[] data = {5, 10, 3, 7, 8, 1, 9};
        print_data(data);
        quick_sort(data, 0, data.length-1);
        print_data(data);
    }
}

quick_sortメソッドの中からquick_sortメソッドを呼び出している。つまり再帰呼び出しである。 quick_sortメソッド内のその上の部分は、分割の際にピボットの左側に小さなデータ、右側に大きなデータとなるようにデータを移動する処理である。

課題2

1000個のデータを乱数で作り、それをバブルソートとクイックソートでそれぞれソートするプログラムを作成せよ。

課題3

課題2のそれぞれの方式においてデータの交換が何回発生するかをカウントし表示せよ。データ列は10個の場合、100個の場合、1000個の場合、10000個の場合をそれぞれ求めよ。

探索のアルゴリズム

データ列の中に望みのデータが入っているかどうかを検査することを探索(search)という。探索はソートと同様にアルゴリズムで良く取り上げられる。なお、探索で探したいデータのことをキーと呼ぶ。

線形探索

一番簡単に探索する方法は、データ列の先頭から順番に探しているデータが入っているか調べることである。これを線形探索という。線形探索は以下のようなプログラムとなる。

public class LinearSearchTest {
    static boolean search(int[] data, int key) {
        int i;
        boolean r = false;
        for (i = 0; i < data.length; i++) {
            if (data[i] == key) {
                r = true;
                break;
            }
        }
        return r;
    }
    public static void main(String[] args) {
        int[] data = {5, 10, 3, 7, 8, 1, 9};
        if (search(data, 10)) {
            System.out.println("探しているデータが見つかりました");
        } else {
            System.out.println("探しているデータは見つかりませんでした");
        }
    }
}

課題4

上記のプログラムでは、繰り返しの度に i < data.length と、 data[i] == key の2つの比較を行っており効率が悪い。そこで以下に説明する番兵を用いて data[i] == key の比較のみで済むようにプログラムを書きかえよ。

データ列の最後にキーと同じデータ(番兵)を付け加える(配列の大きさは1つ増やさなければならない)。こうしておけば、データ列に探しているデータがなくても、番兵に差し掛かると data[i] == keyが必ず成り立ち、繰り返しを終了できる。繰り返しを終了した後、一致した場所が番兵より前ならデータが見つかった、番兵と一致したならデータは見つからなかったということになる。

二分探索

二分探索は線形探索に比べ非常に高速に探索が行えるアルゴリズムである。

まず二分探索を行う際には、データ列がソートされていなければならない。ここでは、データ列が昇順にソートされているものとする。

まず、データ列のど真ん中のデータとキーを比較する。真中のデータよりキーが小さな値であった場合、探そうとしているデータは真中よりも左にあるはずである。この場合は、真中より左側のデータ列に絞って同様に二分探索を行う。逆にキーが大きな値であった場合、探そうとしているデータは真中よりも右にあるはずである。この場合は、右側のデータ列に絞って二分探索を行う。

このようにして2分の1、4分の1、8分の1とどんどん絞られていく。途中でキーと一致すれば見つかった、1つのデータにまで絞られて一致しなければ見つからなかった、というわけである。

二分探索は以下のようなプログラムになる。ただし、この場合再帰呼び出しを使っているが、実行効率のため通常は再帰呼び出しは使わない。

public class BinarySearchTest {
    static boolean search(int[] data, int key, int left, int right) {
        if (left > right) { // 1つに絞られたが見つからなかった
            return false;
        }
        int mid = (left+right)/2;
        if (data[mid] == key) { // キーと一致した(見つかった)
            return true;
        }
        if (data[mid] > key) {
            return search(data, key, left, mid-1);  // 中央より左側を探索
        } else {
            return search(data, key, mid+1, right); // 中央より右側を探索
        }
    }
    public static void main(String[] args) {
        int[] data = {1, 3, 5, 7, 8, 9, 10};
        if (search(data, 10, 0, data.length-1)) {
            System.out.println("探しているデータが見つかりました");
        } else {
            System.out.println("探しているデータは見つかりませんでした");
        }
    }
}

課題5

再帰呼び出しを使わない二分探索のプログラムを作成せよ。
ヒント:上記のプログラムでleftもしくはrightの値を変えながら繰り返しを行えばよい。

課題6

1000個のデータを乱数で作り、線形探索と二分探索を行うプログラムを作成せよ。キーは、データ列中に存在する場合(場所も乱数で決める)と存在しない場合の２通りを試せ。

課題7

課題6でデータとキーを比較している回数をカウントするようにせよ。データ列を10個、100個、1000個、10000個にした場合の比較回数を求めよ。

データ構造

ここでは代表的なデータ構造としてスタックとキューを紹介する。

スタック

参考：教科書 pp.162-163

スタックは、データが積まれたもので、スタックにデータを積む操作(プッシュ)とデータを取り出す操作(ポップ)の２つが行える。本を平積みしている様子をイメージすると良い。プッシュはスタックに既に積まれているデータの上に積む。また、ポップはスタックに積まれている一番上のデータを取り出す。

スタックは、後に入れたデータが先に取り出されるのでLIFO(Last In First Out)と呼ばれる。

ここでプログラムの例を示す。

public class Stack {
    int[] stack;
    int top;
    Stack(int size) {
        stack = new int[size];
        top = 0;
    }
    void push(int data) {
        stack[top] = data;
        top++;
    }
    int pop() {
        top--;
        return stack[top];
    }
    public static void main(String[] args) {
        Stack s = new Stack(1000);
        s.push(50);
        s.push(90);
        System.out.println(s.pop());
        System.out.println(s.pop());
    }
}

なお、上記のプログラムではオーバーフロー(スタックが一杯になる)、アンダーフロー(空のスタックにポップしようとした)の処理をしていない。

課題8

上記のスタックのプログラムで、オーバーフロー、アンダーフローが起きた時にエラーメッセージを表示するようにせよ。また、その場合にプログラムが異常終了しないようにせよ。

キュー

参考：教科書 pp.164-165

キュー(待ち行列)は、スタックと似ているが、先に入れたデータが先に出てくる点が違う。これをFIFO(First In First Out)という。スーパーのレジの待ち行列を思い浮かべれば良い。

キューにデータを入れる操作をエンキュー、データを取り出す操作をデキューという。

以下にプログラムの例を示す。

public class Queue {
    int[] queue;
    int tail;
    Queue(int size) {
        queue = new int[size];
        tail = 0;
    }
    void enqueue(int data) {
        queue[tail] = data;
        tail++;
    }
    int dequeue() {
        int v = queue[0];
        for (int i = 1; i < tail; i++) {
            queue[i-1] = queue[i];
        }
        tail--;
        return v;
    }
    public static void main(String[] args) {
        Queue q = new Queue(1000);
        q.enqueue(50);
        q.enqueue(90);
        System.out.println(q.dequeue());
        System.out.println(q.dequeue());
    }
}

なお、上記のプログラムではオーバーフロー(キューが一杯になる)、アンダーフロー(空のキューにデキューしようとした)の処理をしていない。

課題9

上記のキューのプログラムで、オーバーフロー、アンダーフローが起きた時にエラーメッセージを表示するようにせよ。また、その場合にプログラムが異常終了しないようにせよ。

課題10

上記のキューのプログラムでは、デキューする度に、キューに入っている全データを１つずらす処理を行っていて効率が悪い。教科書にあるリングバッファを使用する方法に書きかえよ。

ソフトウエア入門

ohmi@rsch.tuis.ac.jp