2.4 2次元の座標変換
2次元の座標変換を考える。変換には、移動、スケーリング(縮小・拡大)、回転などがある。これらの変換を一まとめに表現できる方法として、同次座標(homogenous
coordinate)がある。
点[x y]は同次座標では[x y 1]と表現する。また、同次座標で点[X Y W]は普通の座標系では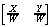 となる点を表しているものとする。このWは倍率(重み)の役割をしている。W=0なら無限遠点を表現することになる。変換前の座標をP[x y]、変換後の座標をP'[x' y']とすると、変換は次のように表せる。 となる点を表しているものとする。このWは倍率(重み)の役割をしている。W=0なら無限遠点を表現することになる。変換前の座標をP[x y]、変換後の座標をP'[x' y']とすると、変換は次のように表せる。
a) 移動(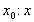 の移動量, の移動量,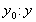 の移動量) の移動量)
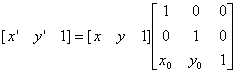 (2.2) (2.2)
すなわち、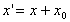 、 、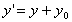
b) スケーリング(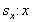 の倍率、 の倍率、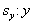 の倍率) の倍率)
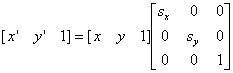 (2.3) (2.3)
すなわち、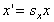 、 、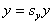
c) 回転(θ:回転角)
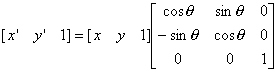 (2.4) (2.4)
すなわち、
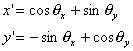 (2.5) (2.5)
このように、同次座標を使うと、多くの変換を統一的な3×3の変換行列の形式で書ける。また、多くの変換を続けて行う際、変換行列を予めかけ合わせることができる。例えば、-60度回転した後[1
2]ほど移動を考える。まず、回転行列は次式となる。
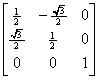 (2.6) (2.6)
また、移動の変換行列は次式である。
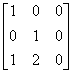 (2.7) (2.7)
したがって、両者の積を用いて次式の変換行列が得られる。
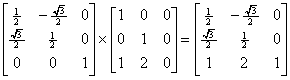 (2.8) (2.8)
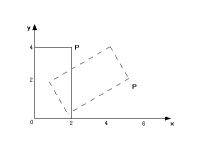
図2.4: 2次元図形の回転移動
図2.4にオリジナルの長方形およびその回転後の図形(図中の点線)を示す。例えば、点P[2 4]は、式(2.8)から変換後は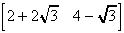 となる。 となる。
(d) アフィン変換
2次元アフィン変換の一般型は次式で表せます。
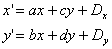 (2.9) (2.9)
(ただしa,b,c,d,D_x,D_yは定数、)上式において、a=b=1,b=c=0のときは平行移動、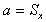 , ,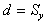 , ,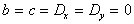 のときは拡大・縮小となります。したがって、アフィン変換は、拡大・縮小、反転などの変換と平行移動が結合された変換です。図2.5にアフィン変換の例を示す。 のときは拡大・縮小となります。したがって、アフィン変換は、拡大・縮小、反転などの変換と平行移動が結合された変換です。図2.5にアフィン変換の例を示す。
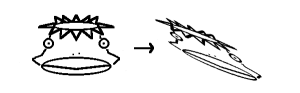
図2.5: アフィン変換の例
| 
