

モデルを作る方法については前章で述べたが、そのモデルをどの位置から見るのか、どのような照明を当てるのか、といった条件を指定して、コンピュータに画像を作らせる作業がレンダリングである。レンダリングでは、光源から出た光がどのようにモデルに当たって目に入るのかを、コンピュータの中で計算によって再現する。つまり、CGの画像生成は基本的にはコンピュータによる光のシミュレーションである。ところで、空間も光も連続的につながったものである。一方コンピュータは、有限の時間に有限の回数の計算しか行うことができず、また連続的な量を直接扱うことができない。そこで空間も光もいくつかの部分に分け、それぞれを1つずつ処理していかなければならない。このため、限られた計算量の範囲内で、モデルをなるべく正確に表した画像を作るための多くの手法が考えられた。
本章では、これらの代表的な手法について述べ、さらに立体表示の試みについても解説する。

3次元物体について、より現実感の高い写実的な表示を行うためのレンダリング法について概説する。
![]()
写実的表示法(2Dと3D)
ここでは、3次元空間に配置された3次元物体の表示法を論じる。
コンピュータ内で生成された3次元データは、最終的にはディスプレイ上に表示されたりして可視化されるが、その際は、3次元の対象を2次元平面上に表示することになる。したがって、2次元平面に限定された範囲で、まるで3次元のような現実感のある写実的な表現が要求される。
3次元物体を2次元上で厳密に表示する方法として、従来は平面図、側面図、正面図のいわゆる3面図が用いられていた。しかし、こうした表示法は、建築や機械などの専門の設計者でなければじゅうぶんに把握できない。また、照明設計にもCGが応用されるようになっており、設計結果の照度分布を等高線として表示したりするが、これも専門家でなければじゅうぶん把握することは困難である。また、たとえ専門家であっても、一目で理解できるようなリアルな表示ができれば、設計ミスに気づきやすいし、デザインのよしあしの評価も容易にできるであろう。もちろん一般の人にとっても有用であるのは言うまでもない。このようなことから、近年では、写真のように写実的な画像を生成する「フォトリアリスティックな画像生成」がCGの中心的な研究課題となってきた。
図5.1に、多面体を表示した例を示す。図の(a)はワイヤフレーム表示といわれ、多面体のすべての稜線を表示したものである。図の(b)は、本来は見えない線を消去して表示したもので、このほうがわかりやすい表現になる。(c)のように陰影を付加するとより写実的となり、さらに(d)では材質感を表現するための模様が付加されている。
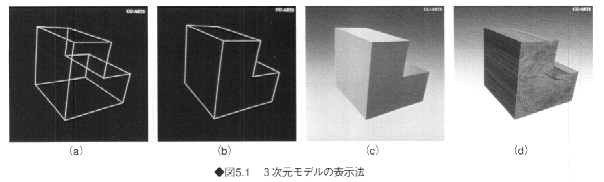
ここで、リアルさはどのようにして得られるかを考えてみよう。リアルさを決定する要素には、遠近感、可視面表示、複雑な形の正確な表示、物理則に基づく輝度計算などがあげられる。
遠近感は、透視投影(「3-4投影変換」参照)によって近くのものを大きく、遠くのものを小さく表示することによって得られる。また、遠くのものがかすんで見えるような大気の効果を表示することも有効である。特殊な例ではステレオグラフィックスまたは立体視(「7-6ステレオグラフィックス」参照)がある。
可視面表示については、見えない線や面を消去して表示する隠線消去・隠面消去とよばれる手法が開発されている。
複雑な物体の形の表示では、多角形だけでなく、曲面の表示や、表面の複雑な模様や凹凸の表示(テクスチャマッピング、バンプマッピング)、山のような複雑な起伏の表示(フラクタル)、樹木など植物の表示、髪の毛のように微細な物体の表示など、さまざまなものが試みられている。また、人体のように滑らかな自由曲面の表現に適したメタボール法も開発されている。
物理則に基づく輝度計算は、リアルさの追求で最も重視されているものである。表示しようとする物体の材質(表面の反射率)、その照射光および反射光が視点に入射するまでに通過する媒質(一般に空気)の物理的・光学的特性を忠実にシミュレートすることで、フォトリアリスティックな画像が得られる。光学的な効果で考慮される要素には、表面の反射特性(材質、表面仕上げ)、光源の種類とその周波数特性、リアルな影(影とその周囲が滑らかにつながっている)、壁などからの反射光(間接光)、レンズなどによる集光効果、大気中の粒子による散乱や吸収(霧や霞など)、空や雲の色、虹、炎や煙、肌の色、回折効果など多くのものがある。
フォトリアリスティックな画像を得るには、物理現象を、いかに計算に適するようにモデル化するかが問題である。一般に、リアルさを追求することは計算時間が増加することに等しいから、逆にリアルさは計算時間に制約されるともいえる。本章では、おもに可視面表示と輝度計算について論じる。
![]()
3Dレンダリングの手順
3次元コンピュータグラフィックス(CG)は、コンピュータ内に定義された3次元の形状モデルをディスプレイのスクリーン上に表示することである。モデル(形状および面の性質)が定義された後、視点、視野範囲、光源の種類と位置が与えられると、スクリーン上の各画素での可視面上の色を求めて表示するという手順がとられる。
まず、形状をコンピュータに記憶しなければならない。これは、頂点の3次元座標とそのつながり(稜線および面)として記憶される。次に3次元物体を2次元平面に表示するために投影を行う。そのための基本的技術として、座標変換、隠線消去・隠面消去、クリッピング(視野内の物体を切り取る)、陰影処理、光の反射・透過・屈折と光源の特性(色と種類)を考慮した輝度計算が必要である。
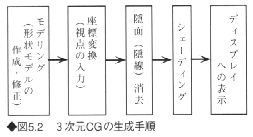
図5.2に、3次元CGの生成手順の概略を示す。データを入力し、その形状をコンピュータ内に内部表現する過程をモデリング(modeling)とよぶ。座標変換は、移動、回転および投影を含む。
線画として表示する場合には隠線消去が、陰影画像なら隠面消去が施され、最後にシェーディングされて、ディスプレイに表示される。座標変換、隠面消去、シェーディングを含めてレンダリング(rendering)とよぶ。3次元CGシステムでは、形状データを作成するプログラムであるモデラと、表示するプログラムであるレンダラに分割されているものも多い。
![]()
属性

シェーディングを行うには、3次元の形状モデルだけでなく、それに付随する物体表面の材質のような、いわゆる属性(アトリビュート)のデータが必要である。属性としては、面の色を計算するための反射率、透過率、屈折率や、場合によって模様や凹凸のデータも必要である。シェーディングを行う対象によってその手法にも違いがあり、物体表面の窓のようにある領域のみ色が異なるものでは、長方形などの多角形とその内部の色(反射率)で指定され、木目や服の図柄のようなものは、テクスチャとよばれて写真画像などが使用される。なお、反射率は一般にR、G、Bの各色成分で指定される。
シェーディングには、物体の情報のほかに、物体を照射する光源の特性も重要である。光源の種類(平行光線点光源など)、明るさ、色(周波数特性)の指定が必要になる。
![]()
現実感のある写実的な表示の第一歩が隠線消去である。ここでは隠線消去の基本的な考え方について解説する。
隠線消去とは
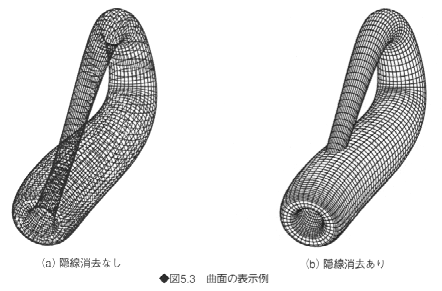
透視投影だけでは、投影されたすべての面が表示され、面どうしが重なってしまう。人間の目に映るのは、そのうちの最も手前の面や稜線であるから、本来は見えない線を検出して表示しないようにする。これを隠線消去(hidden line removal)という。これによって3次元形状がよりわかりやすくなる。図5.3は曲面を表示した例である。
![]()
隠線消去の方法
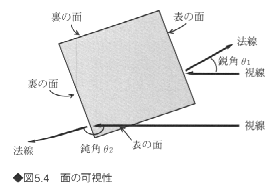
CG研究の創世期である1960年代は、隠線消去の研究が主流であり、多くの手法が開発されたが、1970年代からはリアルな陰影画像の表示に主眼がおかれるようになってきたので、ここでは隠線消去の基本的な考え方を説明するにとどめる。面の可視性について考えると、面の法線ベクトルと視線との角が鋭角である面は見え、それが鈍角のものは見えない(図5.4)。これらの面はそれぞれ表の面(front
face)および裏の面(back face)といわれる。図5.5の例では、面S1は表の面(θ1<90゜:θは面の法線と視線方向との角)、面S2は裏の面(θ2>90゜)である。
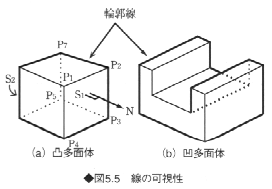
面および稜線の可視性については次の性質がある。
①表の面に属する稜線は可視であるが、2つの裏の面の共通の稜線は不可視である。図5.5(a)の例では、稜線P1P4は表の面どうしの稜線なので可視、稜線P5P7は裏の面どうしの稜線なので不可視である。
②表の面と裏の面との稜線のつながりを輪郭線という(図の太線)。凸多面体の輪郭線は1つで、かつ凸多角形である(図の(a))。
③表と裏の面の角度が凸の場合の稜線は一般に可視(同図(b)の太実線)であるが、凹稜の場合は不可視(同図(b)の太破線のうちの長い方)である。
なお、一般に裏の面は隠線処理の前に取り除く。複数個の凸多面体が存在し、それらが投影面上で重ならないなら、上記の性質のみで可視性の判定はじゅうぶんである。また、多面体どうしが重なるかどうかは、それらの輪郭線が重なるかどうかで判定することができる。凹多面体の場合は複雑となるが、ここでは省略する(詳細は文献1)を参照されたい)。
上記の処理において必要な、面の法線ベクトルの算出法について述べる。図5.5(a)の面S1は,頂点P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)などを含んでおり、これらの頂点は多面体外部から見て右回りに与えられている。またこの多面体は凸多面体である。このときには、面の法線N(Nx,Ny,Nz)を、次のように2線分の外積によって求めることができる。
![]()
すなわち、法線のx、y、z成分は次式で求まる。
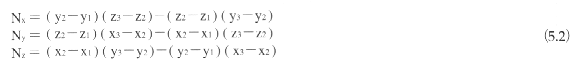
面の向きの判定は次のように行う。面が表の面か裏の面かは、面の法線Nと視線ベクトルVとの内積で判定できる。すなわち、視点をP0(x0,y0,z0)とすると、(P0-P1)Nの値が正なら表、負なら裏の面である。あるいは、次式の関数を用いて判定することができる。

すなわち、D(x0,y0,z0)の符号で判定できる。ここで、D=0は面の方程式(ax+by+cz+d=0)と等しく、(a,b,c)は前述の法線ベクトル(Nx,Ny,Nz)に一致する。
透視変換後の座標で多面体が与えられているときは、面の法線のz成分の符号で判定することもできる。また、凸多面体の場合には、簡単な方法として、投影後もP1、P2、P3が右回りなら表の面と判定できる。

3次元CG処理のなかで最も基本的な手法である隠面消去法の代表的なアルゴリズムであるZバッファ法とスキャンライン法について解説し、さらに並列演算が可能かつ効果的なレイトレーシング法について紹介する。
![]()
隠面消去とは
図5.1(b)のように、不可視の面を検出して消去することを隠面消去(hidden surface removal)という。これらの判定のための基本的な性質を述べる。
凸多面体が1つの場合は、表の面を表示すればよいが、複数の多面体が重なり合う場合を含めて考えると処理は複雑になり、種々の方法がある。これらの方法では一般に裏の面は隠面消去の前に取り除く。
隠面消去については多くの手法が開発されており、これを判定を行う空間について分類すると、
画像空間アルゴリズム(image space algorithm)
物体空間アルゴリズム(object space algorithm)
優先順位アルゴリズム(priority algorithm)
に分けられる。
画像空間アルゴリズムと物体空間アルゴリズムの違いは、それぞれ判定をスクリーン上で行うか、3次元空間で行うかである。
優先順位アルゴリズムは、3次元空間で多角形の前後関係を求めておき、スクリーン上で遠方のものから順に重ね描きする方法である。つまり物体を構成する多面体または多角形に、与えられた視点にもとづいて優先順位を与え、優先順位の低いものから順にフレームバッファに書き込むもので、最終的にはスクリーンに可視面が表示される。ここで優先順位とは、視点に対して近いものほど順位が高いものとする。この方法で重要なことは、優先順位をいかに決定するかである。なおこの方法は最近ではあまり使われていない。
画像空間アルゴリズムは、スクリーン上の領域(画素または走査線)を単位に隠面消去を行う。この方法の代表的なものにZバッファ法がある。n枚の多角形をN×Nのサイズのスクリーンに表示する場合について、処理時間を考えてみると、画像空間アルゴリズムでは、nN2に比例した時間を要する。物体空間アルゴリズムでは、面の交差判定などを行うとき、n面と残りのn-1面とで判定するから、n2に比例した時間が必要である。
![]()
Zバッファ法
Zバッファ法(Z-buffer algorithm)は、表示しようとする面のZ値(視点からの奥行き)を各画素ごとに蓄える方法である。奥行き(depth)情報を利用することから、デプスバッファ法ともよばれる。
まず、各々の面を投影面に投影し、その面が占める画素の位置に、その面のZ値を格納する。このとき、すでに格納されている面があれば、そのZ値と比較し、小さいほう(すなわち手前)の面の情報を記憶する。
各画素について奥行きを記憶するZバッファ(Z buffer)と、画像(表示する色)を記憶するフレームバッファ(frame buffer)を準備しておき、次の手順で計算する(図5.6参照)。
①スクリーンの全画素を背景色に初期化する。また、Zバッファの全画素を最遠点(Z=∞)に初期化する。
②面をスクリーンに表示するとき、計算点のZ値が以前に書き込まれていたZ値より小さければ、すなわち新しい点が視点から見て手前にあれば、Z値を更新する。
③同時に、フレームバッファに蓄えているその点における画素の色も更新し、それを表示する。
④表示すべきすべての面の全画素について処理を行うと、最終的に隠面消去した画像が得られる。
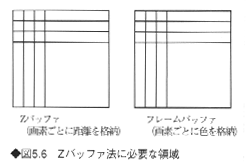
この方法では、スクリーンヘの表示が処理する面の順序に行われる。
多角形は走査変換によって塗りつぶす。上から下へと処理する場合、ある走査線と多角形の1辺との交点をxiとすると、その次の走査線と辺との交点は次式によって求められる(図5.7参照)。
![]()

ここで、mは辺の傾きである。このように加算のみによって交点を算出できる。交点xi、xi+1での奥行きZも同様に加算のみで算出できる。さらに、走査線上の2交点間の奥行きについても加算のみで算出できる。すなわち、2交点間の奥行きの差を交点幅で割った値を△zとすると、画素kでの奥行きZkから、隣接画素(k+1)での奥行きzk+1は次式で算出できる。
![]()
このように、加算によって順次値を求めていく方法を増分法という。
たとえば、奥行きは次のように求めることができる。面の方程式は、
![]()
で表される。これは前述のD(x,y,z)=0と等しく、(a,b,c)は面の法線のx、y、z成分に相当する。面を透視変換した後の座標系(視線方向がz軸となっており、視点が原点)で表したものとすると、スクリーン座標(x,y)での奥行きzは、上式を変形し次式によって求められる。
![]()
なお、前述の△zは-a/cに等しい。曲面の場合は、その処理はやや複雑である。上のように、スクリーン座標から奥行きを簡単には求められない。比較的簡単な方法として、キャットマル(Catmull)は、曲面を再帰的に分割し、分割後の微小パッチが1画素程度になったら、そのときのxy座標でスクリーン上の位置を、またz座標を奥行きとして利用する方法を開発した2)(この方法が最初のZバッファ法である)。
多角形の場合は、Zバッファ法はアルゴリズムが簡単で、ハードウェア化に向いている。また、この方法は大きな記憶容量を必要するが、メモリの低価格化にともない、グラフィックワークステーションでリアルタイム処理が可能なハードウェアとして、標準装備されることが多くなった。
メモリに制限がある場合は、画面をいくつかの領域に分割し、各領域でZバッファ法を適用する。また、走査線単位にZバッファ法を適用する方法もある。
この方法は、各画素ごとにZ値を求めるので、複数の面が相互に干渉する場合でも適用できる。しかし、影や反射・屈折の処理は困難である。また、エリアシング(面の境界が階段状のギザギザを生じる)の問題(「2-5-5アンチエリアシング」参照)も残る。
![]()
スキャンライン法
スキャンライン(scanline)とは走査線のことで、走査線単位に隠面消去する方法をスキャンライン法という。走査線をスクリーンの上から下へ走査しながら、走査線と視点を含む平面(走査面またはスキャンライン平面とよぶ)を作る。この平面によって物体をスライスし、その交線を抽出し、それらの可視部分を表示する方法である。
このアルゴリズムの手順は次のとおりである(図5.8参照)。
①物体を投影し、y座標の大きい順にソート(並べ替え)する。y座標の最大値・最小値によって物体と交差する走査線の範囲がわかる。
②走査面と物体との交線(セグメントとよぶ)を求め、各セグメント端点のx座標によって、xの小さい順にソートする。
③セグメント端点によりサンプルスパン(図5.8(b)参照)を定める。各サンプルスパンにおいて奥行き方向でセグメントが重なるときは、z方向の最大・最小テストによって、セグメントどうしの前後関係を求め、可視セグメントを表示する。
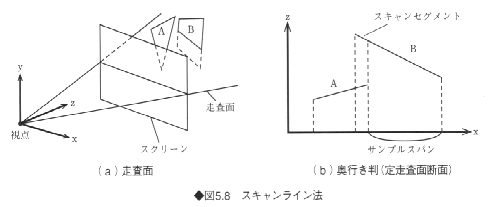
③の処理において、各走査線に対する隠面消去には、走査線1本分のZバッファ法を用いる方法もある。隠面消去された物体がスクリーン上に表示される様子を図5.9に示す。物体は一般に何本か連続した走査線にまたがって存在する。また、ある走査線と次の走査線における可視面は類似している〈このように類似していることをコヒーレンス(coherence)という〉。そこで、前の走査線に対する可視面情報を記憶しておくと、次の走査線の可視面(走査線と面との交点)の計算に利用できる。この方法は、アルゴリズムは複雑であるが、Zバッファ法ほどの記憶容量は必要とせず、レイトレーシング法より速く処理できる。

![]()
レイトレーシング法
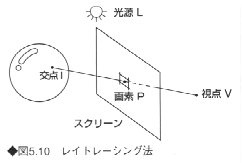
レイトレーシング法(ray tracing algorithm)は、光線追跡法または視線探索法ともよばれ、各画素ごとに視線を発生し、すべての面について、視線と最初に交わる点を探索する方法である(図5.10)。この方法は、アルゴリズムがきわめて簡単で、さらに曲面や鏡面反射、透過・屈折効果など、光の複雑な現象の表現に向いている。
《1》レイトレーシングのアルゴリズム
レイトレーシングは次の手順で行う。
①視線(図5.10中の視点Vと画素Pを通過する直線)は、スクリーン上のある画素を通って物体方向に向かう。この視線と交差する別の物体があるかどうか調べる。
②交差する物体が存在するなら、視線と物体との交点(図中1)を求める。交差する物体が複数ある場合には、すべての物体について交点を求める。交点がない場合には背景の色とする。
③視線と交点との距離を求め、最も視点に近い物体を抽出する(隠面消去したことになる)。
④可視物体の輝度の計算をする。このとき、光源と交点を結ぶ線分と交差する物体を調べ、影の有無を判定する。
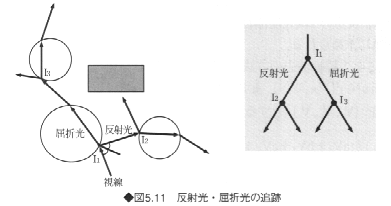
⑤反射・屈折がある物体なら、反射方向、屈折方向を求め、これらの方向を視線とみなして②③の処理を行い、屈折・反射して見える物体を抽出する(図5.11)。
以上の処理をスクリーン上のすべての画素について行う。
⑤の処理では、視線(レイ)と交差する物体が不透明物体の場合には、「5-4シェーディング」で述べる陰影計算によって物体の色を計算し、画素Pに塗る。一方、鏡面のような反射面に視線が交差した場合には、さらに反射方向を追跡する(図5.11)。また透明物体の場合には、屈折方向も追跡する。反射と屈折方向の両方を求める必要がある場合が多い。光線の反射や屈折方向を求めるには、その面の向き(すなわち法線)を求める必要がある。また、屈折方向を求めるには、法線方向のみだけではなく、その物体の屈折率が必要である(「5-4-5透過・屈折光」参照)。視線が反射と屈折の2本の線に分岐することから、追跡経路は2分木表現される(図5.11)。
レイの追跡の終了条件は次のとおりである。
①レイが拡散面に当たった場合
②レイがいずれの物体にも交差しない場合(背景の色とする)
③反射または屈折の回数が指定したものより多くなった場合
④反射や減衰により光の強さが小さくなった場合
《2》レイと物体の交差判定
レイと物体との交差判定の代表的な例として、まず球について説明する。
図5.12に示すように、視点をPv、視線単位ベクトルをV、球の中心をRc(xc,yc,zc)、球の半径をRとする。球の方程式は
![]()
である。視線の直線方程式はパラメータt(視点からの距離に相当)を用い、
![]()
となる。この式のPのx、y、Z成分を球の方程式に代入すると、
![]()
となる。この式でA=1、B=((Pv-Pc)・V)、C=|Pv-Pc|2-R2とおくと、
![]()
と書ける。レイと球が交差するための判別式は、上式が解をもつ条件から、
![]()
である。したがって、交点までの距離を表すtは、上の2次方程式の2つの解の小さいほう、すなわち次式となる。
![]()
(tが負のときは、背後にあることになるので、交点としては使えない)
このtを用いれば、交点の3次元座標およびその点での曲面の法線が求まる。球の場合、法線は交点と中心から簡単に求められる。

平面の場合は、「5-2-2隠線消去の方法」で述べた関数Dを利用できる。D(x,y,z)(=ax+by+cz+d)は平面から点(x,y,z)までの距離を表している。したがって、視点座標を(xv,yv,zv)、視線ベクトルを(Vx,Vy,Vz)とすると、交点でのパラメータtは次式で求まる。
![]()
自由曲面の交点計算の場合、厳密には高次式(双3次曲面の場合18次式)を解く必要がある。したがって、多角形近似を行うことが多い。比較的精度よく交点を求める方法は、次の2つに大別できる。すなわち、各レイに対して、曲面を再帰的に画素のサイズになるまで細分割する方法と、数値解法(ニュートン法など収束計算)を用いる方法である。
レイトレーシング法の開発者として知られるホワイテッド(Whitted)3)は、前者の方法を利用した。すなわち、曲面を再帰的に4分割し、分割後の曲面を包含する球とレイが交差したら、曲面とレイが交差したとみなす。一般に、自由曲面はパラメトリック曲面で、u、vパラメータを用いて表現される。そこで、交点での(u,v)座標を求め、これから3次元座標および法線を求める。
《3》高速化
レイトレーシング法は計算時間の膨大さが欠点であるが、高品質の画像生成に適するため、多くの研究発表があり、交点を見つけるためのアルゴリズムや、交点テスト回数の軽減策などが開発されている。高速化の代表的な方法としては、次のものがある。
(1)バウンディング・ボリューム(bounding volume)
各物体を球や直方体のような簡単な形状(バウンディング・ボリュームとよばれる)で囲っておき、レイとバウンディング・ボリュームとの交点があるかどうかを調べる。図5.13は物体を包含する球をバウンディング・ボリュームとし、これとレイとの交差判定を行う状況を示す。バウンディング・ボリュームとの交点がない場合には、そのレイと物体が交差する可能性はない。バウンディング・ボリュームとレイとの交点がある場合のみ、物体とレイとの交差判定をすればよい。

(2)空間分割法
あらかじめ3次元空間を細かく分割し(図5.14)、どの空間にどの物体が存在するかを記憶しておく。レイを追跡するとき、そのレイが通過する部分に存在する物体のみと交差判定すればよい。

(3)並列計算
各画素で独立に計算できることから、複数個のCPUをもつコンピュータによる並列計算も試みられている。一般にはプロセッサの数に比例して速くなるが、限界はある。最近では、超並列コンピュータを利用する試みもなされている。

3次元CGにおいて、より写実的な表示を行うためには、光源の効果を無視することはできない。ここでは、ある光源のもとでの物体の明るさや色を決定するためのアルゴリズムについて解説する。
![]()
シェーディングとは
3次元物体を観察するには、光源が必要である。ある光源のもとで物体を観察すると、その表面の明るさが場所によって微妙に異なっている。面の向きと光の照射方向により面の明るさは変化し、光のあたらない部分もある。この部分を陰(shade)という。また、この物体があるために他の物体上に光があたらない領域を生じることがある。この領域を影(shadow)という(図5.15)。CGでは、こうした陰影の効果を計算することが必要である。
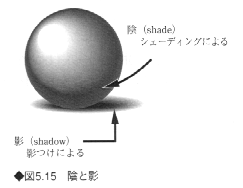
陰影表示は、光のあたり具合いによって色調が変化する状態を表示するシェーディング(shading)と、光が遮られて生じる影の表示法(shadowing)の2つから成る。物体の光学的特性に依存して生じるさまざまな現象や、遠近感の表示法など多くの手法が開発されている。
精密な物理法則に従うほど写実的な画像を創成できるが、それだけ高速、大容量のコンピュータを必要とする。したがって、どのような物理モデルを採用するかは生成する画像の用途に依存する。
《1》シェーディングモデルの要素
シェーディングのために採用する光の物理モデルをシェーディングモデルという。シェーディングモデルを構成する要素は、物体を照射する光源の種類およびそれらの特性、物体を照射する光(直射光と間接光)の種類、さらに、反射・透過・屈折などの物体の性質である。
物体を照射する光は直射光と間接光に分けられる。直射光はさらに平行光線(太陽光)、点光源(電灯、スポットライト)、大きさをもつ光源(蛍光灯、間接照明)に分けられる。大きさをもった光源として線光源、面光源などがある。間接光としては、一般に環境光として一定値を与えるが、厳密な方法として、相互反射光を考慮する場合がある。
被照面の反射光は、拡散反射成分と鏡面反射成分から成り、ほとんどの物体は両成分を含んでいる。拡散反射はすべての方向に同一強度で反射するもので簡単であるが、鏡面反射は複雑である。図5.16にこれらの要素を考慮した球の表示例を示す。

《2》シェーディングモデルの発展
1960年代後半から1970年代を通じての、平行光線と点光源による簡単な陰影表示技法の基礎開発段階から、1980年代に人って、各種の配光特性をもった点光源をはじめ、線光源で表した蛍光灯、面光源による埋め込みパネル、多面体光源に対する表示法が開発されるようになった。
鏡面反射は、一般にフォン(Phong)のモデルが使用されているが、金属を表現しやすいブリン(Blinn)のモデル、およびクック・トランス(Cook-Torrance)のモデルも使用されるようになった。異方性反射モデル(同一方向に磨いた金属や布地の表現)も注目されてきている。表面の特性だけでなく、反射・屈折後の光の表示も重要である。曲面からの反射光が他の面に照射した光の分布や、水面による屈折光(集光効果など)も表示されている。物体表面からの反射のみでなく、大気や水中の粒子による散乱・吸収光の計算も行われるようになった。夜間街灯など強い光に対して、目の瞳孔やまつげによって光の回折が起こり、虹のような色が見える現象の再現も試みられた。さらに、相互反射光を計算するラジオシティ法が開発された。
![]()
環境光
環境光(ambient light)は間接光ともよばれ、一般には画面全体に一定の明るさを与える。すなわち、環境光は、入射角に関係なくいずれの方向にも同じ強さで反射するものと考える。この環境光による反射光の強さIは次式によって与えられる。
![]()
ここで、Iaは入射光の強さ、kaは反射率である。一般に、影の領域にもある程度の明るさを与えるために、環境光が用いられる。
さらに精密なモデルとして、直射光によって照射される面から反射する2次反射光以上の相互反射光(「5-4-8ラジオシティ法」参照)や天空光を考慮した間接光の計算法も開発されている。
![]()
拡散反射光
拡散反射(diffuse reflection)光は、入射した光があらゆる方向に同じ強さで反射するもので、石膏や白墨(チョーク)のように表面がざらざらしたものにみられる。拡散反射光は、表面から入射した光が物質内で多重散乱した後、表面に出た光である。鏡面反射成分がまったくなく、拡散反射成分のみの面は、完全拡散面(あるいは等方拡散面)とよばれる。以下に、光源の種類に応じた拡散反射光の計算法を説明する。
《1》平行光線
太陽のように無限遠点に光源が存在する場合、その光は平行光線とみなされる。あるいはレンズによって平行光線を作ることもできる。
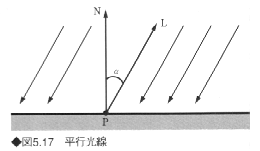
平行光線の場合、反射光の強さは入射角の余弦(cos)に比例する。この法則をランバート(Lambert)の余弦則という。平面を平行光線で照射した場合、面上のどの点でも反射光の強さは一定である。図5.17の場合、入射光の強さをIiとすると、反射光の強さIは次式で表せる。
![]()
ここで、αは入射角、すなわち面の単位法線ベクトルNと光線の方向を示す単位ベクトルLとのなす角であり、kdは面の拡散反射率である。なお、cosαはNとLとの内積によって求まる。
《2》点光源
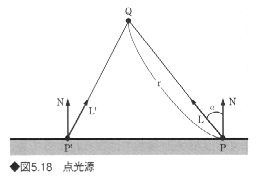
現実の世界では、すべての光源は大きさをもっているが、光源が小さく比較的物体から離れている場合は、点光源とみなすことができる。点光源の場合には、光のエネルギーが距離の逆2乗則およびランバートの余弦則に従う。図5.18の場合、光源Qの光度をIq、とすると、点Pでの反射光の強さは、
![]()
となる。ここでαは面の法線Nと光線のなす角で、kdは拡散反射率、rは光源と計算点Pとの距離である。一般にはIqは一定値が用いられる。この式でわかるように、同じ平面上でも点ごとに反射光の強さが異なる(図のPとP'では反射光の強さは異なる)。
実際の光源は、それぞれ固有の配光特性を有している。すなわち、光源の光度が灯軸と光の放射方向の角度θによって異なる。光源の配光特性を考慮すると、より多様な表現が可能になる。実際の配光は複雑なので、簡易な表現法が試みられている。たとえば、配光特性を灯軸からの角度θの関数Iq(θ)で表して、Iq(θ)=1/2L(1+cosθ)(I0は灯軸方向の光の強さ)などが用いられた。図5.19は、どのような配光をもつ点光源が適当かを検討するためのCG画像の例である。
《3》大きさをもつ光源
現実の光源はすべて大きさをもっているが、ここでは、光源の大きさを無視できない場合について考える。大きさをもつ光源には、線光源、面光源、多面体(曲面体)光源、および天空光がある。
大きさをもつ光源のある点での輝度は、図5.20(a)に示すように、光源を単位半球表面に投影し、さらにそれを半球底面に投影した面積A'に比例する。この計算は複雑であるが、多角形光源に対しては次の解析解が得られる。大きさをもつ光源の代表的なものは面光源である。m角形の光源を考え、光源の単位面積あたりの光度をLとすると、ある点での反射光の強さIは次式の境界積分法によって求まる(図5.20(b)参照)。


ここで、βIはPQI、PQI+1のなす角で、δIは三角形PQIQI+1の法線と面の法線との角である。
多面体光源の場合は、点Pからこの多面体光源を眺めたときの可視面をそれぞれ面光源と考え、すべての可視面に対する反射光の強さを総和すればよい5)。
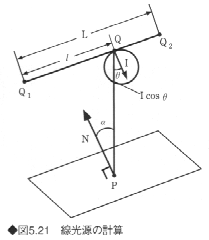
線光源は、点光源が直線上に連続的に並んでいるものと考えることができる。また、光の放射する強さは、線光源に垂直な方向とのなす角θの余弦(cos)に比例する。したがって、ある点Pの反射光の強さIdは、線光源の単位長さあたりの光度をIq、光源の長さをLとすると、次の積分式で表される4)(図5.21参照)。

天空光は、半径の大きい半球光源とみなすことができる。天空は非常に大きいので、任意の計算点はつねに非常に大きいドームの中心にあると考えてよい。前述の面光源では一様の輝度分布としたが、天空の明るさは一様ではなく、太陽位置(時刻、季節)、天候によって変化する。天空光を考慮することにより、窓からの採光予測などに利用できる。
![]()
鏡面反射光
拡散反射光が物質内での多重散乱による光であるのに対して、鏡面反射(specular reflection)光は、物質の表面での直接反射によって生じる。よく磨かれた陶器などが照射された場合、鏡面反射により表面の一部にハイライトを生じる。鏡面反射光は、入射角と反射角が等しい正反射の方向に光が最も強く反射される。完全鏡面反射でないものは、正反射方向の近傍にも反射される。なお、曲面のハイライトは、それを調べることによって曲面の加工精度を検査することができるので、工業デザインではとくに重要である。
![]()
《1》フォンのモデル7)
視線と正反射方向のずれ角γによる鏡面反射成分の減少の割合をcosnγで近似する方法である(図5.22)。鏡面反射光の強さをIとすると、Iは次式で求められる。
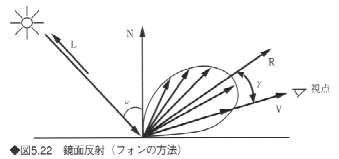
ここで、Iiは入射光の強さ、γは正反射方向と視線との角である。Wは鏡面反射率で、入射角αの関数である。Wは厳密には入射角や波長によっても異なるが、一般に一定値(W(α)=ks)を用いることが多い。nはハイライトの特性を示すもので、nが大きいほどシャープなハイライトが得られる。図5.23にnを変化させた場合の比較を示す。

《2》金属の反射モデル
ブリンおよびクックとトランス8)は金属に適した反射モデルを開発した。より厳密な物理法則に基づくため、反射面と視線との角度、表面の粗さによる鏡面反射成分の分布特性を考慮したものである。ブリンは、物体表面を微小な面の集合と考え、その微小な面の方向が、面の法線ベクトルの方向を中心にある分布をしているものとした。この分布としては、ガウス分布あるいは回転惰円体を仮定した。これらの関数は次に定める方向ベクトルHの関数とした。光の光線ベクトルをL、視線をVとし、これらの2等分ベクトルをHとする(図5.24参照)。
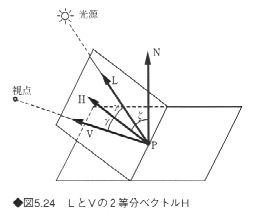
すなわちHは次式で与えられる。
![]()
クック・トランスのモデル8)は、反射率分布関数を改良し、さらに波長および入射角に依存することも考慮し、反射率はフレネル(Fresnel)の式を用いた。とくに金属の表示に適しているが、よりいっそう計算時間は長くなる。反射率は次の式を用いた。

ここで、πは物体表面の粗さの度合いを示す値、Gは幾何学的減衰因子、Fはフレネルの反射率、Dは分布関数である。微小面の分布は次のベックマン(Beckmann)分布関数Dで近似した。

ここで、ξは上のHと法線Nとの角であり、mは適当な定数で、mが小さいほどシャープな分布となる。
![]()
透過・屈折光
よく磨かれた物体表面の鏡面反射による映り込みや、透明物体の透過、屈折現象を計算する方法として、レイトレーシング法がある(「5-3-4レイトレーシング法」参照)3)。レイと物体との交点が求められたとき、画素に塗る色Iを決定するためのモデルは次式で表される。
![]()
この式は、第1項から順に、環境光、拡散反射光、鏡面反射光、屈折光(透過)の成分を示す。Nは面の単位法線ベクトル、Liはi番目の光源の光の入射方向ベクトル、mは光源数、Sは鏡面反射光、Tは屈折方向からの光、ksは鏡面反射率、ktは透過率(kt=1-ks)である。屈折方向はスネルの法則によって求められる。
図5.25に示すように、物体の表面に光が入射するとき、反射光ベクトルをR、屈折光の方向を示すベクトルをP、視線方向をVとすると、RとPは次式によって求まる。

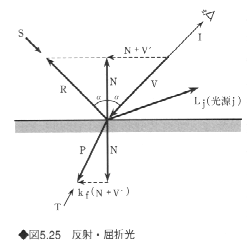
ここで、

ただし、nは物体の屈折率である。
入射角および屈折角の関係はスネルの法則で決まり、次式で表される。
![]()
ここで、n1、n2は入射前および入射後の物体の屈折率である(図5.26)。
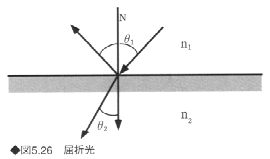
透明な物体に対する反射率は、次のフレネルの式で表される。
![]()
ここで、θ1およびθ2は入射角および屈折角である。また、透過率は、1-反射率kとして求められる。また、次のように変形すると計算しやすい。

ここで、c=cosθi=(L・H)(θiは入射角LとHとのなす角度)、g2=n2+c2-1、nは屈折率の比n2/n1である。
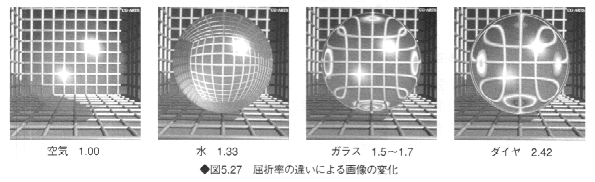
図5.27に屈折率の違いによる画像の変化を示す。また、図5.28は、屈折を考慮した画像で、透明物質中にティーポットが埋め込まれた例を示す(レイトレーシング法で表示)。

![]()
スムーズシェーディング
物体(とくに曲面)上の各点について、その座標値や法線ベクトルを求め、与えられた光源に対する輝度を計算してシェーディングすることは、計算時間の増加を招く。そのため、球や円柱などの2次曲面を用いることが多く、自由曲面は多角形で近似して表示することが多い。しかし、多角形として輝度を計算すると、輝度が滑らかに変化しないため不自然な画像となる。これは、多角形どうしの境界での輝度差によるものである。人間は、輝度の変化に敏感で、実際の輝度の差よりも大きく感じる。これはマッハバンド効果として知られている(図5.29)。
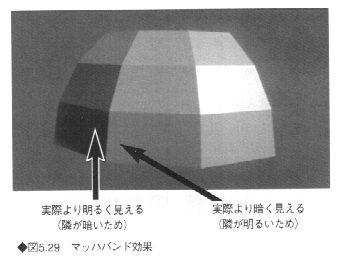
近似的に滑らかに輝度を計算する方法は、スムーズシェーディング(smooth shading)とよばれる。この方法は多角形の頂点での輝度または法線の情報を利用して、多角形内の各画素の滑らかな輝度の変化を計算する方法である。すなわち、曲面を多角形によって近似したとき、多角形の頂点のみにおいて輝度計算し、多角形内では補間処理により内挿する。この方法にはグロー(Gouraud)とフォンの2つの代表的な方法がある。なお、多角形内の輝度を一定値にして表示し、スムーズシェーディングを行わない表示法をコンスタントシェーディングという。
《1》グローのスムーズシェーチィング
輝度の補間によりスムーズシェーディングを行う方法である。
曲面を多角形に分割し、各多角形の各頂点での輝度を求めておく。最初に、多角形と走査線との交点(図5.30の点L、R)での輝度を線形補間によって求め、次に走査線上の各画素(たとえば図のP)での輝度を線形補間により求める。すなわち、走査線y=ysと多角形(たとえば頂点A、B、C、Dよりなる多角形)との交点LおよびRにおける輝度IL、IRは次式によって求める。

さらに、走査線上の点P(xp,ys)の輝度IPは、次式によって求められる。
![]()
ここで、IA、IB、ICおよびIDはそれぞれ点A、B、C、およびDにおける輝度である。なお、輝度を得るには法線が必要であるが、多角形の頂点における法線ベクトルは、その頂点(図5.30(b)の点P)を含むすべての多角形の法線ベクトルの平均値を用いる。
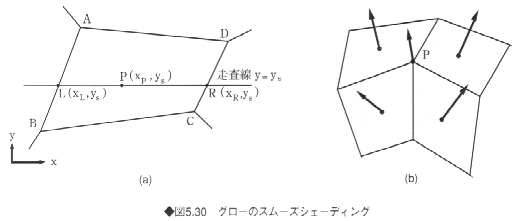
この方法では、輝度のみ補間することから、ハイライトの計算が正しくできない欠点がある。たとえば多角形の内部にハイライトがある場合、頂点のみで輝度を求めたので、いずれの頂点もハイライトには入っていない。そのためそれらを補間しても当然ハイライトは生じない。また、補間は線形補間であるため、多角形どうしの境界部ではスムーズに明るさが変化せず、折れ線的に変化する。すなわち、マッハバンド効果は減少するが、完全にスムーズになるとは限らない。
《2》フォンのスムーズシェーディング
法線ベクトルの補間によりスムーズシェーディングを行う方法である。
曲面を多角形に分割し、各多角形の各頂点での法線ベクトルを求めておく(図5.31)。まず、多角形と走査線との交点(図5.31の点L、R)での法線ベクトルNL、NRを線形補間によって求め、次に走査線上の各画素(たとえば図のP)での法線ベクトルNpを線形補間により求める。すなわち、多角形内の点Pでの法線ベクトルNPを、グローシェーディングと同様な補間法によって求める(IA、IB、IC、ID、IL、IRをNA、NB、NC、ND、NL、NRで置き換えればよい)。
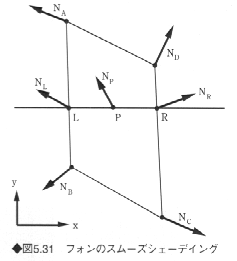
補間により得られた法線ベクトルと光源の位置から、点Pにおける輝度を計算することができる。この方法は、グローの方法に比べてより精度が高く、ハイライトが計算できる。しかし法線を補間する際に、各点での法線ベクトルの正規化が必要で、2乗と平方根の計算が含まれるため、計算時間がかかる。
図5.32に、グローとフォンのスムーズシェーディングの比較を示す。

![]()
影付け
物体によって生ずる影を考慮することはきわめて重要である。それは、物体の高さや相互の位置関係を示すのに重要な役割を果たす。影は写実的な表示にとって欠かせないものであるが、そのアルゴリズムは光源の種類に大きく依存する。
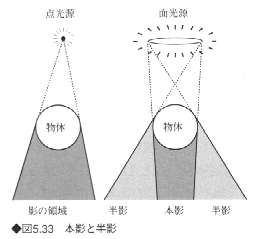
光源からの直射光がまったく当たらない部分を本影といい、環境光を無視すると輝度がゼロになる。平行光線や点光源のような、大きさをもたない光源による影がこれに相当する。大きさをもつ光源による影は本影の周囲に半影を生じる。半影は、光源の光の一部によって照射された領域である(図5.33)。図5.34に、光源の違いによる影の違いを示す。図でわかるように、影の境界部がソフトな半影をもっている。

《1》平行光線・点光源の影
影は本影(直接光がまったく当たらない)のみであるから、比較的簡単に求まる。おもな方法は次の4つである。
(1)レイトレーシング法
最も簡単な方法で、各ピクセルに表示される面の位置と光源を結び、さえぎる物体があるかどうかを調べる。図5.35に示すように、点Bの場合、光源との間に遮蔽物が存在するから影であり、一方点Aは障害物がないので影ではない。この方法は1点1点判定するので、処理時間が長いのが欠点である。

(2)走査線単位の方法
スキャンライン法に適用する方法であり、走査線単位の隠面消去と同時に行われる。光源から見たときの表の面の各辺を、処理しようとする走査面上の可視面へ走査線ごとに投影する方法(図5.36。面S2による面S1上の影の区間P1-P2の計算)で、影の表示法としては初めて開発されたものである。

(3)2段階法
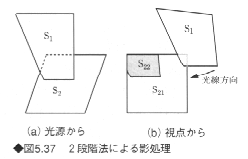
この方法は、スキャンライン法あるいはZバッファ法に適用される。光源と視点からの2つの透視図(図5.37)を求め、表示時に影の領域をマッピングする方法である。第1段階として、物体を光源から見たときに隠される領域(この領域は影となる)を求める(図5.37(b)のS22)。次に、物体を視点から眺め、影の領域をマッピングする。
(4)シャドウポリゴン法
物体データ作成時に、光源と遮蔽物体で発生する影を生じる空間を利用する方法である(図5.38)。この空間をシャドウボリューム(shadow volume)とよぶ。また、シャドウボリュームを構成する面を影多角形という。
ある面上の影の領域は、シャドウボリュームと面との交差部分として求まる。あるいは、計算点がこのシャドウボリューム内かどうかで、影かどうか判定できる。この方法は、走査線単位の方法および2段階法に比べて、余分のデータ容量が必要である。

《2》大きさをもつ光源の影
大きさをもつ光源の影を扱うと、より写実的な画像が得られるが、計算は複雑になる。線光源、面光源、天空光のように光源の大きさを考慮したときは、影はまったく光の当たらない本影の部分と、光源の一部の領域の光が当たる半影の部分に分けられる。
(1)近似的に求める方法
大きさをもつ光源の表面上にいくつかの点光源を配置し、点光源の集合として光源を扱う方法である。この方法は、影を生じさせる物体を検出できないことがあり、計算誤差が大きいという欠点がある。また、光源をある大きさの球と考え、球と計算点によって構成される円錐と物体との交差領域を求め、この交差の程度に応じて影の程度とする方法もある。
(2)積分法によって求める方法5)
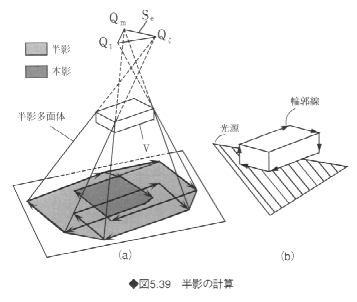
図5.39は、多面体Vが三角形状の光源Seによって照射されたときの、本影と半影の領域を示したものである。図の暗い影の部分は本影、明るい影の部分は半影の領域である。半影中の明るさは、その計算点から光源を見たときの可視部分の大きさに依存する。たとえば、計算点から光源を眺めたとき、図5.39(b)に示す斜線の領域が面光源の可視領域であるから、この可視部分を、新たにその点に対する光源とみなすことによって、計算点での輝度を求めることができる。図5.40は円柱光源および曲面光源を用いた画像の例である。

![]()
ラジオシティ法
りアルな画像を生成する方法として、レイトレーシング法が有名であるが、それと同時にラジオシティ法も注目されるようになってきた。
図5.41のような室内を考えてみよう。室内の各部分での照度は、光源からの直射光成分と、壁などから反射された間接光からなる。この間接光までを含めて考える照明計算を大局照明(global
illumination)という。照明工学の分野においては、光の相互反射の計算は従来から行われていた。また、熱工学分野においても放射伝達の理論は古くから研究されていた。しかし、いずれの分野においても、物体間の反射光(または放射熱)を遮る物体の影響まで考慮した計算法は確立されていなかった。CGの分野には、最初ゴーラル(Goral)が導入し、影の影響も考慮した手法は西田ら5)およびコーヘン(Cohen)ら6)により提案された。

相互反射を考慮すると、従来の方法に比べて次の点においてよりリアルな画像が得られる。
①影が半影(ぼやけた影)を伴う。
②直射光が届かない部分も、相互反射による間接光により照射される。
③反射面の色が隣接する面に影響する(カラーブリーディングとよばれる)。
すなわち、レイトレーシングによる鋭い画像に比べ、間接光がかもしだす柔らかい雰囲気が表現できるのが特徴である。
相互反射の計算法としては、物体の構成面をいくつかの面素(エレメント)に分割して連立方程式を解く方法と、レイトレーシング法を拡張した方法、および両者を組み合わせた方法がある。
面素分割法においては、フォームファクタ(form factor:形態係数)が最も重要な要素である。光源から放射された光が何回か反射された後、最終的に各エレメントの明るさがある値となる。この計算の際エレメント間のエネルギーの授受の割合を決めるのがフォームファクタである。フォームファクタは幾何学的形状のみによって決まるので、光源の光度を変化させても不変である。また、光源が変化しない場合、相互反射の計算を一度しておけば、視点が変化した場合でも再計算しなくてよい。ただし、鏡面反射成分は視点の位置に依存して変化するから、鏡面反射成分を考慮するときの処理は複雑となる。
《1》ラジオシティ方程式
図5.42は、図5.41のうち2つのエレメントの関係(SiとSj)を示したものである。面積AiのエレメントSiから面積AjのエレメントSjへのフォームファクタをFijとすると、エレメントSiでの輝度(またはラジオシティ)Eiは、すべてのエレメントからの反射光を考慮して、次式により表される。
![]()

ここで、ρiは反射率、E0iは放射光(一般に直射光による輝度)、EjはエレメントSjの輝度、nはエレメント数である。この式は、エレメントSiでの輝度が、他のすべてのエレメントからの光の総和に反射率を乗じたものとして得られることを表している。
各エレメントの輝度は、上式から導かれるn元方程式を解くことにより求まる。すなわち、
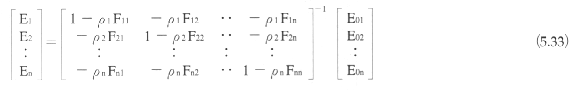
この式は、ガウス・ザイデル法などにより解くことができるが、より効率的に解く方法として、漸進的ラジオシティ法が開発された12)。
《2》フォームファクタの計算
フォームファクタとは、エレメントSiのすべての点から放射されたエネルギーがエレメントSjに受け取られる率を意味し、次式により求まる(図5.41参照)。
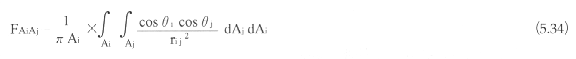
ここで、

の関係がある。たとえば室内に机があるように、一般にエレメント間に障害物(他のエレメント)が存在することが多い。これを考慮するため、次のようにフォームファクタを修正する。
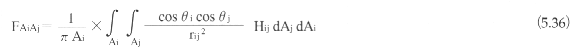
すなわち、エレメント間に障害物があるかどうかを示すHijを導入する。これは、障害物が存在する場合は0で、存在しない場合は1である。言い換えると、Hijは、あるエレメントから他のエレメントが可視であるかどうかを表す。そこで、隠面消去の判定が必要となる。
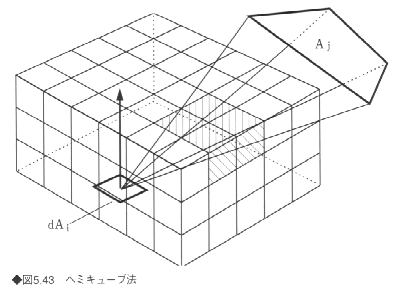
代表的なフォームファクタの方法として、ヘミキューブ(hemi-cube)法がある(図5.43)。この方法は、図5.20(a)の半球を半立方体で近似する方法である。図5.43に示すように、エレメントを中心として半立方体を置き、その各面をメッシュに分割する。この各メッシュに対して、あらかじめフォームファクタ(デルタフォームファクタとよぶ)を求めておく。基本的には、計算点を視点、半立方体の表面をスクリーンと考えた場合のZバッファ法による隠面消去法によって遮蔽効果が求まる。すなわち、影を考慮したフォームファクタは、エレメントの中心から見て、エレメントの可視領域(図の斜線部)が覆うメッシュのデルタフォームファクタを加算することによって求まる。ただし、離散化された点でサンプリングすることから、エリアシングや精度についての問題が生じる。したがって、これを改良した多くの方法が開発されている。
図5.44に、ラジオシティ法による相互反射の計算例を示す。

![]()
大気中の微粒子の光の吸収・散乱は不透明効果をもたらし、遠方の物体の色彩をあせたものにして灰色に近づけ、それによって遠近感を増す。また、大気中の粒子に当たった光の散乱によって、ライトの投射範囲内の空間は明るくなる。自然界では、雲やビルのすき間から差し込む太陽の散乱光を観察することができる。
大気中の微粒子による光の散乱・吸収効果によって、遠方のものほど反射光の彩度が失われる。一般に反射光は距謹が遠くなるに従って指数関数的に減衰し、次式で表わされる。
![]()
ここで、Ciは物体の反射光(CR、CG、CBはそれぞれ輝度の赤、緑、青成分)、C'iは視点に到達した光の色、Fiは無限遠点の大気の色、rは物体と視点との距離、Lは霧の状態によって決まる減衰係数であり、Lが小さいほど霞は深くなる。フライトシミュレータなどでは、霞の効果を計算するのが一般的になってきている。図5.45に霞の効果を計算した画像の例を示す。


簡易的に写実性の高いCG画像を作成する方式がテクスチャマッピングであり、各種の方式が提案されている。ここでは、その基本的なアルゴリズムとその応用例について紹介する。
![]()
テクスチャマッピングとは
マッピング(mapping)とは、「地図を作る」という意味のほかに、数学の「写像、座標変換」の意味がある。CGでは後者の意味で、2次元の平面上にある絵柄や模様などを3次元曲面や平面の上に貼り付けることをマッピングという。ここで、貼り付ける模様のことをテクスチャといい、2次元テクスチャを3次元曲面などに写像することをテクスチャマッピング(texture
mappmg)という(図5.46)。この作業は曲面上の1点とテクスチュア上の1点とを対応づけることによって行うことができる。2次元の平面であるテクスチャ空間と3次元の曲面である物体空間との対応づけの方法としては、
①投影による方法
②極座標変換などを用いる方法
③マッピングパラメータを曲面データに付加する方法
などがあるが、ここでは最も一般的な③の方法について具体的に述べる。

3次元CGでよく用いられる曲面には、球面、円筒面などのほかに、ベジェ曲面などのパラメトリック曲面がある(4-4-5「パラメトリック曲面」参照)。パラメトリック曲面では、xyz座標系における曲面上の点を、以下のような媒介変数を用いた形で表す。
ベジェ曲面(図5.47)では曲面Lの点の位置ベクトルSは次式で求められる。
![]()
ただし、

であり、これをブレンド関数とよぶ。
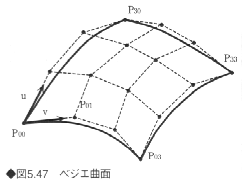
uおよびvは媒介変数(パラメータ)であり、これらを0≦u≦1、0≦v≦1の範囲で変化させることによって曲面上の点の座標を得ることができる。また、Pijは曲面の形を制御する点の位置ベクトルである。
この媒介変数は曲面上の座標系を表しており(uv座標系)、これをマッピングのための座標として利用する。実際には、曲面を構成するポリゴンの頂点にこの媒介変数の値、すなわち曲面上の座標値を付加しておく。図5.48に示すように、ある正方形のテクスチャの3次元曲面へのマッピングを考えると、曲面上のu、vの値の示す正方形上の座標値のテクスチャデータを貼り付ければよいことになる。図5.49にテクスチャマッピングの作品例を示す。

マッピングを用いることによって、CGで用いる3次元の曲面の形状とテクスチャを分けて考えることができるので、同じ形状にさまざまなテクスチャを貼り付けることは容易に行える。ただし、平面上の情報を曲面の上に貼り付けるので、テクスチャが歪んでしまうといった欠点があるため(地球儀と世界地図の関係を想起されたい)、テクスチャをなるべく歪まないようにマッピングする手法が研究されている。また、これらのマッピングの技術をいくつか合わせて使用することにより、テクスチャの形や色などの複数の要素を合成したマッピングも可能である。

![]()
テクスチャの生成
テクスチャをCGで表現するためには、何らかの形でコンピュータにテクスチャの情報を入力しなければならない。そのための方法として、以下の2つが考えられる。
《1》写真などの画像を直接利用する方法
スキャナなどによりテクスチャ画像をコンピュータに入力することによる、比較的簡単な方法であり、写真などのもつリアリティをそのまま生かせるという点で有用な方法である。しかし、ある条件下で撮影された写真などを直接用いるため、CGによる視点や光源の移動に対しては対応が難しく、不自然な画像が生成されることがある。これは、視点や光源がその写真が撮影されたときと異なった状況の3次元CGを作ろうとした場合に生じる問題で、単一の条件下での画像のみではこれを回避することはできない。
《2》コンピュータによってテクスチャを生成する方法
この方法は、テクスチャ生成の手順を構成しておいて、コンピュータにテクスチャを自動生成させるものである。コンピュータの中にテクスチャの色や形状のデータをもっているので、任意の視点や光源位置でのCGを作ることができる。
テクスチャ生成のために構成された手順にはいくつかのパラメータが含まれており、これをうまく設定することにより、対象とするテクスチャの特徴を表現することができる。また、パラメータなどの変更によって、類似したテクスチャヘの拡張が可能なものが多く、その有効範囲は広い。テクスチャ生成の過程で乱数やフラクタル、1/f揺らぎなどを導入することにより、生物特有の不規則さや自然物らしさの表現、個体差などの表現も可能である。
テクスチャの生成手順の構成には、テクスチャの種類によってさまざまなアプローチが考えられる。たとえば、貝殻の模様やウロコの模様などでは幾何学的なアプローチが有効であり、格子模様やボロノイ分割(グラフ理論に基づく平面分割法)などによってテクスチャが生成可能である。
また、生物のもつテクスチャの生成規則のモデルを導入した研究も報告され、生成されたテクスチャの生物学的な妥当性についても興味がもたれるようになってきている。たとえば、キリンやシマウマなど動物の体表面の模様が、生物テクスチャの生成規則のモデルの1つである「反応一拡散(reaction-diffusion)」とよばれる考え方を用いて生成できるという報告もある。
![]()
バンプマッピング
バンプマッピング(bump mapping)は、物体表面こテクスチャの凹凸をマッピングし、これにより物体表面の法線ベクトルを傾かせることで、シェーディングにおいて擬似的に細かな凹凸を表現する手法である(図5.50)。この場合、テクスチャの値はR、G、Bといったカラー値ではなく、凹凸を表現する高さデータとなる。
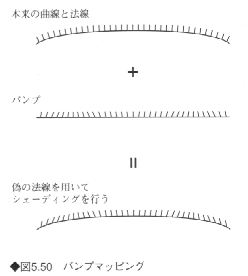
マッピングされるテクスチャの点について、その高さデータのu方向、v方向の傾きdu、dvをそれぞれ求める。マッピング先の物体表面での法線ベクトルをN、u方向およびv方向の単位ベクトルをu、vとすれば、シェーディングのための擬似的な法線ベクトルN'は以下のように求められる。
![]()
バンプマッピングの例として、皮革テクスチャをハンドバッグにマッピングした例を図5.51に示す。

バンプマッピングではこのように高さデータから法線を求めることが一般的であるが、法線ベクトルの(x,y,z)の値をテクスチャデータとしてもち、法線ベクトルを直接マッピングする方法もある。しかしながら、この場合には当然データ量は3倍になる。また、高さデータをマッピングする方法をディスプレースメントマッピングとよんで、法線ベクトルのマッピングでないことを明示することもある。
![]()
環境マッピング
物体の存在する3次元空間内に半径無限大の仮想球を考え、その内面にあらかじめ環境のテクスチャを貼り付け、金属などの物体表面にそのテクスチャが反射しているように表示を行うことを環境マッピングという。反射方向ベクトルは視点の位置と物体表面の点の座標で決まり、このベクトルからテクスチャ上の座標が決定できる。環境テクスチャを貼り付ける形状は、球のほかに円柱や立方体なども用いられることがある。
円柱の場合の例を図5.52に示す。同図(a)では、まず3次元空間の中心から見た環境を円柱の内面に写像することで環境テクスチャを生成し、その後、同図(b)における物体表示の際に、適切な環境テクスチャを物体表面にマッピングする。

環境のテクスチャには画像取り込みによる方法も用いられるが、あらかじめCGによりレンダリングしたり、ペイントシステムにより風景画を作成して用いることもある。その際には、上下左右前後の6面を立方体に写像したり、その立方体を球状に変換して用いることもある。
環境マッピングはこのように、金属の表面などでの光の反射を簡易に表現することが可能であるが、原理上1回の反射のみ表現可能であり、多重反射など複雑な現象を扱うことは不可能である。したがって、環境マッピングではレイトレーシングのように物体どうしが互いに映り込むようなシーンを表現することはできないことになる。環境マッピングの作品例を図5.53に示す。

環境マッピングは物体表面での反射を扱うため、リフレクションマッピング(reflection mapping)ともよばれる。これに対し、透明あるいは半透明な物体を表現する際の光の屈折を表現するマッピングをリフラクションマッピング(refraction mapping)という。これは環境マッピングと同様に、3次元空間内に半径無限大の仮想球を考え、その内面にあらかじめ環境のテクスチャを貼り付け、ガラスなどの透明物体で屈折して見えるテクスチャを物体表面に表示するものである。リフラクションマッピングの概略を図5.54に示す。ガラスなどの物体表面の点Pで屈折した光は環境テクスチャが貼り付けられた仮想球と点Qで交わるので、その値を用いて点Pのシェーディングを行う。
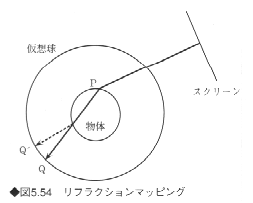
厳密には物体の反対側でも屈折は起こるので、点Q'のテクスチャを使うべきであるが、点Qを用いても屈折の効果はある程度表現できるので、一般には点Qが用いられる。リフラクションマッピングも環境マッピングと同様に、1回の屈折のみが表現可能であり、レイトレーシングのような反射と屈折が多重になっているような画像は生成できない。
![]()
ソリツドテクスチヤリング
テクスチャを2次元データとしてでなく、3次元的な関数として貼り付けることをソリッドテクスチャリング(solid texturing)という。木材や大理石などの模様は、ある1つの面から隣接する面にもつながっており、各面ごとに通常のテクスチャマッピングを行ったのでは、面の境界で不連続となり、正確な模様を表現することが難しい(図5.55(a))。このような場合に、3次元的にテクスチャが定義されているソリッドテクスチャリングが有効であり、任意の断面で切断しても連続した模様を表示させることができる(図5.55(b))。木目の場合には、放射状の正弦波関数を基に、それに揺らぎを付加することで自然な木目を生成することができる。ソリッドテクスチャリングによる表示例を図5.56に示す。



従来の3次元CGのデータは、主としてポリゴンとして面単位で与えられていた。それに対して、3次元空間内の点ごとにある物理量が与えられたデータに対して、直接可視化する方法として、ボリュームレンダリングがある。ここでは、そのアルゴリズムと応用例について紹介する。
![]()
ボリュームレンダリングとは
X線CT(ComputedTomography)を利用すると、人体内部を輪切りにして断層像として表示することができる。この断層像は、断層面上の各点でのX線吸収量を表している。断層面を少しずつ移動させて得られた断層像を積み上げることにより、人体を上下、左右、前後にそれぞれ一定間隔で分割してできる、各ボクセルに対するX線吸収量を3次元配列に格納したようなデータが得られる。このようなデータをボリュームデータとよび、測定方法によっては、ある空間(ボリューム)内に分布する特定の物質の濃度や密度などを表すことができる。
ボリュームデータをもとに、たとえば骨格を表示するとき、従来のCGの技法では、まず骨の表面の形状を決定してから、レイトレーシングなどのレンダリングアルゴリズムを適用する必要があった。しかし、'場所によっては骨はきわめて複雑な形をしており、また骨とそれに隣接する組織で、X線の吸収率が滑らかに変化することもあり、骨、筋肉、内臓などを明確に分離することは難しい。
このようなとき、骨の表面の形などを決定することなく、ボリュームデータから直接に組織を描画する方法をボリュームレンダリング(vo1ume rendering)という。ボリュームレンダリングの医用画像以外への応用としては、大気中の水蒸気の濃度分布を用いて雲を表示した例がある。
![]()
ボリュームレンダリングの手法
ボリュームレンダリングでは、3次元空間内に分布している特徴量を、任意の視線(レイ)に沿って一定間隔でサンプリングし、その値を加算していくことで最終的に半透明な画像を生成する。レイに沿ってボリュームをサンプリングすることをレイキャスティング(ray casting)という。ボリュームレンダリングの概念を図5.57に示す。レイは投影面上の各画素から射出され、一定間隔でボリューム内のボクセルをサンプリングしていく。
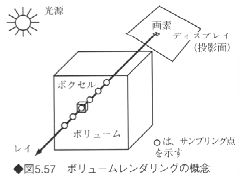
ボリュームレンダリングでは、半透明表示を行うことで内部を可視化するが、これは各ボクセルに不透明度αを与えることで実現している。不透明度αはボクセルの値そのものを用いることもあるが、隣接するボクセルの値からの勾配に基づいてαを決定する方法も提案されている。
表示対象としている物体表面に対応するボクセルのαを大きくすることで、その対象を不透明に近く、強調して描画することが可能となる。レイキャスティングでは順次各ボクセルの輝度値とαとの積を加算していき、αの総和が1となるか、またはレイが対象としているボリュームから抜け出たとき、その画素に対する処理を終了し、加算結果をその画素の値として表示する。現在のサンプル位置での輝度値と不透明度をそれぞれi、α、この点に入射した積算輝度値をIinとすれば、このサンプル点を抜けたときの積算輝度値Ioutは以下の式で表される。
![]()
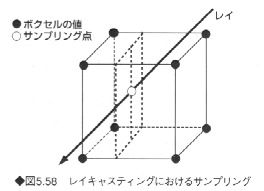
レイキャスティングにおけるサンプリング点での輝度値と不透明度は、一般に、隣接する8つのボクセルの各々の値から線形補間により求める(図5.58)。
一般的なボリュームレンダリングの処理手順を図5.59に示す。CT画像や各種物理量分布のシミュレーション結果などで得られた3次元ボリュームデータに対して、まず、前処理では雑音除去や画像強調などが実行される。ここではボリューム全体を対象とした3次元画像処理が行われることもある。次に、各ボクセルの輝度値と不透明度を決定し、レイキャスティングにより各画素に対する最終的な輝度値を求める。これらの値の決定がボリュームレンダリングでは重要となる。

《1》輝度値
各ボクセルの輝度値iは、隣接するボクセルの値からの勾配より推定される法線ベクトルNを用いて、フォンのシェーディングモデルから次式のように計算される。
![]()
ここで、Iは光源強度を、ka、kd、KsはそれぞれCGで通常用いる環境光、拡散光、鏡面反射光成分の割合を表す。dは投影面からボクセルまでの距離を表し、k1およびk2は投影面に近いものほど明るく表示するデプスコーディング(depth coding)法のパラメータである。Lはボクセルから光源への単位方向ベクトル、Hは正反射光を求めるためのベクトルで、レイの方向である視線方向ベクトルVにより次式で求められる。
![]()
ボリューム内のあるボクセルf(i,j,k)の法線ベクトルNは次式で求められる。
![]()
ここで、▽f(i,j,k)はこのボクセル値のx、y、z方向の勾配として以下のように求められる。
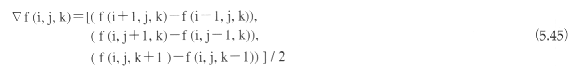
各ボクセルには色属性値を与えることもでき、その場合には、光源の色特性とボクセルの色値の積として、色を含めた輝度値を決定する。色を扱う場合にはR、G、Bの3原色で計算する方法があるが、より厳密には可視光領域でのスペクトル特性を考慮する必要もある。
《2》不透明度

先に述べたように、不透明度αとしてボクセルの値そのものを用いることもできるが、ボクセル値に加えて隣接するボクセルの値からの勾配に基づいてαを決定する方法も提案されている。勾配値を考慮するのは、異なる成分との境界を強調することができるからである。
いま、成分の境界となるボクセル値fと不透明度αが図5.60のように与えられているとする。このとき、任意のボクセル値fをもつボクセルの不透明度αは、勾配と図から補間された不透明度の積として次式で与えられる。
《3》ボクセル値を不透明度とするボリュームレンダリング法
雲などを表示するときには、ボクセル値である水蒸気密度が光を散乱・減衰させる要因となる。また、各ボクセルの輝度値は、光源からボリューム内を通過して来た光がそのボクセルで反射・散乱して視点方向に向かう光の量として表される。したがって、投影面からレイキャスティングを行う前に、光源からのレイキャスティングによって各ボクセルの輝度値を決定しておく必要がある。
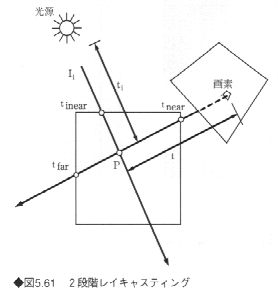
図5.61にこの2段階レイキャスティングの様子を示す。いま、レイ上で視点からの距離がtの点P(x(t),y(t),z(t))を考え、そこでのボクセル値をf(x(t),y(t),z(t))、各光源の光がボリューム内の減衰を受けて点Pに届く光量の和である輝度値をI(x(t),y(t),z(t))とすれば、対応する画素値Bは次式で求められる。

ただし、tはボクセル値を減衰係数に変換する定数、p(cosθ)はフェーズファクタ(phase factor)とよばれ、各ボクセルからの光が視点方向に向かう割合を示し、光源方向ベクトルと視線方向ベクトルとのなす角度θの余弦の関数として与えられる。
ここで、点Pの輝度値IはPから各光源へのレイ上での減衰を考慮することにより次式から求められる。

輝度値Iの計算法は、このほかにもボリューム内を一様媒体と仮定する方法などが提案されている。ボリュームレンダリングを用いた表示例として、水蒸気分布を与えた雲を図5.62に、X線CTによる人体内部像を図5.63に示す。

![]()
ボリュームの構成要素であるボクセルに対して、通常のボクセル値に加えて異方性反射特性をもたせることにより、動物の毛皮などの質感を表現することが可能となった。新たに考案されたこの構成要素をテクセル(texel)といい、式(5.47)のフェーズファクタに代えて異方性反射分布をする関数ψを導入することで次式のように実現している。

カジヤ(Kajiya)は、異方性反射特性を有するテクセルとして微小円柱を用い、微小円柱の長さ方向と、光源、視点の単位方向ベクトルT、L、Eを基に、拡散光と正反射光を計算し、それらの和をψとして動物の毛皮の質感表現を行った(図5.64)16)。
(1)拡散光
光源は微小円柱の半分の面のみを照らし、照らされた円柱面上の点での拡散光強度は、ランバート(Lambert)のモデルより、
![]()
で与えられる。
ここで、kdは拡散反射係数、Nはその点での単位法線ベクトルである。
したがって、この微小円柱から放出される全拡散光成分ψdiffuseは次式で与えられる。
![]()
図5.64においてベクトルTに直交する平面PヘベクトルLを射影し、その単位ベクトルをL'、ベクトルTとL'に直交する単位ベクトルをBとすれば、以下の関係式が得られる。


これらを式(5.51)に代人すれば、
![]()
となり、拡散光成分は光源方向ベクトルLと微小円柱の長さ方向ベクトルTとの角度の正弦(sin)に比例することになる。
(2)正反射光
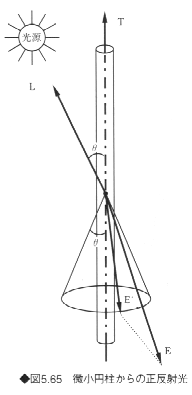
図5.65に示すように、微小円柱の長さ方向に対し角度θで入射した光は、入射角度と同じ角度をもつ円錐の上を正反射すると仮定する。したがって、正反射光成分ψspecularは次式で与えられる。
![]()
ただし、ksは正反射係数、Eは視線方向ベクトルであり、E'はEに最も近い円錐上の正反射光ベクトルである。pはフォンのモデルにおける正反射光の拡がりを表す係数である。
【参考文献】
1)中前,西田3次元コンピュータグラフィックス昭晃堂,(1986).
2) E. Catmull, A Subdivision Algorithm for Computer Display of Curvecl Surfaces, Proc. IEEE Conf. on Computer Graphics, Paftern Recognition and Data Structures, pp.309-315 (1975) .
3) T.Whitted, An Illumination Model for Shaded Display, Comm. ACM, Vol.23, No.6, pp.343-349 (1980) .
4) T.Nishita, I.0kamura, E.Nakamae, Shading Models for Point and Linear Sources, ACM Trans. on Graphics, Vol.4, No.2, pp.124-146 (1985) .
5) T.Nishita. E.Nakamae, Half-Tone Representation of 3D Objects Illuminated by Area or Polyhedral Sources , Proc. COMPSAC '83, pp.237-242 (1983) .
6) T.Nishita, E.Nakamae, Continuous Tone Representation of ThTee-Dimensional Objects 11luminated by Sky Light, Computer Graphics, Vol.20. No.3, pp.125-132 (1986) .
7) Bui-Tuong Phong, I1lumination for Computer-Generated Pictures, Comm. ACM, Vol.18, No.6, pp.311 -317 (1975).
8) R.Cook. K.Torrance, A Reflectance Model for Computer Graphics.ACM Trans. on Graphics. Vol.1 , No.1, pp.7-24 (1982) .
9) H.Gouraud, Computer Display of Curved Surfaces, IEEE Trans. Computer, Vol.C-20, No.6, pp.623-628 (1971) .
1 O) T.Nishita, E.Nakamae, Continuous Tone Representation of Three-Dimensional Objects Taking into Account of Shadows and Interreflection, Computer Graphics, Vol.19, No.3, pp.23-30 (1985) .
11) M.F.Cohen, D.P.Greenberg, The Hemi-cube: A Radiosity Solution for Complex Environments, Computer Graphics, Vol.19, No.3, pp.31-40 (1985) .
12) M.F.Cohen, et al., A Progressive Refinement Approach to Fast Radiosity Image Generation. Computer Graphics, Vol.22, No.4, pp.75-84 (1988).
13) T.Nishida, O.Miyawaki, E.Nakamae. A Shading Model for Atmospheric Scattering Considering Luminous Intensity Distribution of Light Sources. Computer Graphics, Vol.21 , No.3, pp.303-310 (1987).
14) A.Witkin, M.Kass: Reaction-Diffusion Texiures, Computer Graphics. Vol.25, No.4, pp.299-308 (1991).
15) Arie Kaufman: Volume Visualization, IEEE Computer Society Press, California (1991).
16) J.T.Kajiya, T.L.Kay: Rendering Fur with Three Dimensional Texturres, Computer Graphics, Vol.23, No.3, pp.303-310 (1989) .
17)増田千尋:3次元ディスプレイ,産業図書,(1990).
18)大越孝敬:三次元画像工学,朝倉書店,(1991).
19)特集「立体感と3次元情報」,テレビジョン学会誌,Vol.45,No.4,(1991).
20)舘,廣瀬=バーチャル・テック・ラボ,工業調査会,(1992).