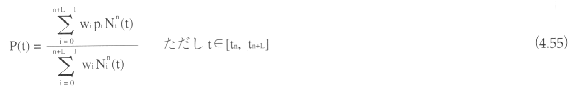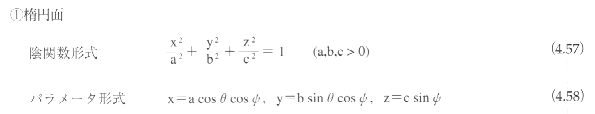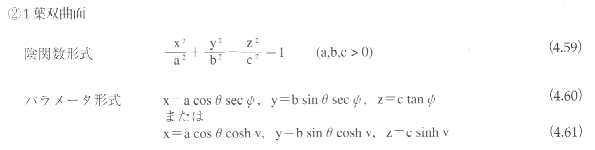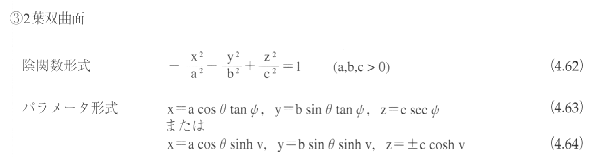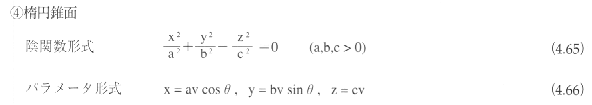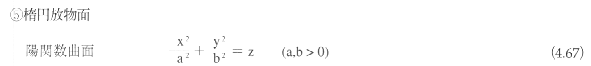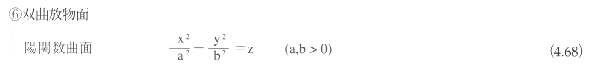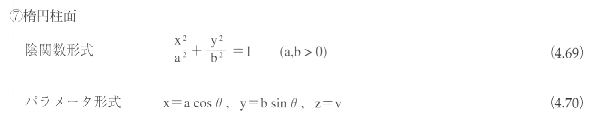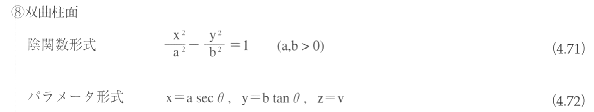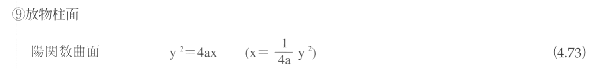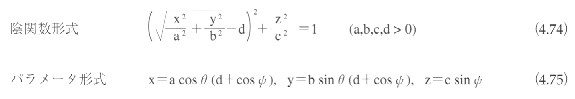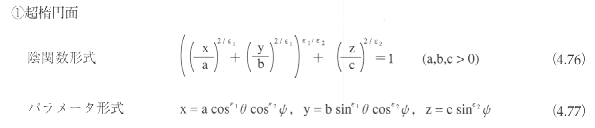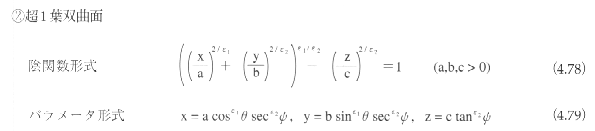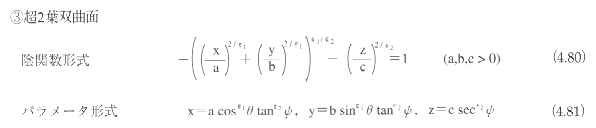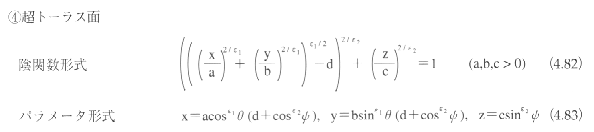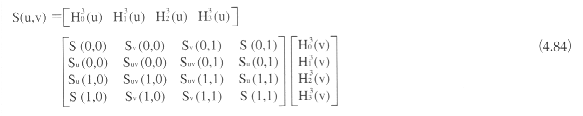モデリングという作業を、CGによって自動車の絵を作ることを例に考えてみよう。
人は「自動車」といえばそれがどんなものであるかを直感的に理解するが、コンピュータではそうはいかない。そこでまず、大きさ、形、色、材質、場合によっては名前、用途、価格といったデータをコンピュータに与える必要がある。画像を作るという目的にとっては、とくに大きさ、位置、形、色、表面の反射率などが重要である。このようなデータをコンピュータに与える作業をモデリングという。また、コンピュータに蓄積されたチータの集まりをモデル(この例では自動車のモテル)という。モデルができたら、次にそれをどの位置から見るかを指定し、画像を作る作業に移る。
本章では、モデリングに際しての注意事項、コンピュータ内部で形を表現したり生成するためのきまざまな手法、曲線や曲面の表わし方について述べる。

モデリングやレンダリングを行うとき、でき上がった画像がそれを見る人によって正しく認識されるかどうかを考慮することが必要である。この部分では、さまざまな形と、それを人間がどう認識するのかを考える。
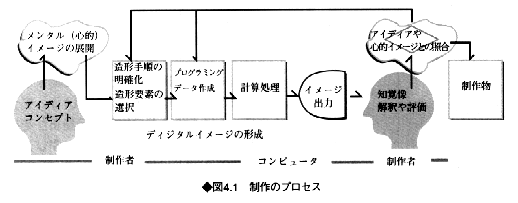
 制作のプロセス
制作のプロセス
コンピュータによって画像を制作するときには、まず漠然としたアイディアやイメージをもとに、具体的な形や処理手続きを明確にし、考え方や造形要素を整理して、コンピュータで処理できる手順として組み立て直す必要がある。そしてこの手順に従って、プログラミングやデータの作成を行い、コンピュータによる処理の結果をモニタやプリンタに出力する。さらに、この生成された画像が、はじめのアイディアやイメージをよく表しているかどうか評価する。うまく表現していない場合には、データや造形プロセスの変更を行い、意図したイメージにより近いものを求めていく。
こうした一連のプロセスを経てコンピュータによる画像が制作される。
制作においては、形態のもつ意味や、心的な効果も考慮しながら画像の評価を行うのであり、モニタ上に画像を描くことがすべてではない。アイディアを具体化する際のイメージの構造化、表示法、および見る側の反応などといった要素も検討しなければならないのである(図4.1)。
 造形の手順
造形の手順
アイディアをもとに心的なイメージを具体化するための手順について考えてみよう。
制作を始めるにあたって、イメージが比較的はっきりしている場合は、点や直線、円弧、曲線、長方形、多角形などを組み合わせて、意図した形を決定する。もし3次元のものを対象にするなら、錐体や柱体、球などの基本形態(プリミティブ)を組み合わせたり、断面の形状を設定した回転体や、底面を設定し高さ方向に平行移動する方法などによって、意図した形に近づけていく。このような方法は形状指定型とよぶことができる。
一方、イメージが初めから明確になっていなくても、さまざまな画像生成の手法を試みることによって、次第に表現意図にふさわしい形ができ上がったり、逆に最初の意図を超えて効果的な形が生まれたりすることもある。このような場合は、画像生成の条件やパラメータなどをいろいろ変更しながら、でき上がる画像を表現意図との関係で評価していく作業となる。これを手続き指定型とよぶことができる
。
 造形要素
造形要素
人と人とのコミュニケーションにおいては、伝達したい内容を、音声、身振り、絵や図などによって記号化する。一方、情報の受け手は視覚や聴覚を通してこれらを認識し、さらにその意味の解釈を行う。とくに視覚記号によるコミュニケーションは、意味を直感的に理解できるという点で、きわめて有効な手段である。
コンピュータは、定規やコンパス、絵具などの従来からの手段に代えて、造形のための新たな道具を提供した。コンピュータは、従来の方法では困難であった各種のパターンを作り出し、繊密で正確な出力を可能にし、またアニメーションによる時間的要素の導入など、表現の世界を飛躍的に拡大させた。コンピュータによる画像の形成においては、漠然としたイメージではなく、表現したい対象を明確にし、その造形要素は何かを明らかにする必要がある。その根幹にあるものは、数理的な造形能力とともに豊かな感性や創造力であると言っても過言ではない。それによってはじめて意味概念の記号化とその解釈において、情報の送り手と受け手の間で共通の理解をもつことができ、スムーズなコミュニケーションが可能となる。
ここでは、画像形成の基礎となる造形要素についてとりあげる。
《1》点・線それらの意味するもの
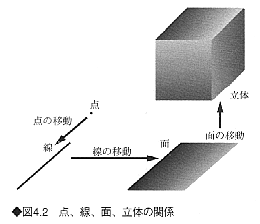
幾何学的には、点は面積をもたず、位置のみを示す。この点が移動した軌跡が線である。さらに線の移動によって面が形成され、面を移動させることで立体を作ることができる(図4.2)。
以上が幾何学的な図形の概念であるが、われわれは、視覚を通して図形を認知し、さらにその解釈を行う。そのため、点や線に大きさや色を付与したり、たとえば複数個並べたりすることで、図形の意味を感じたりしている。点や線のもっているこうした意味について、いくつかの例をあげてみよう。
(1)方向を示す
等間隔に置かれた点は正方形のパターンに見えるが、点を置く間隔を変化させることによって方向を示すことができる(図4.3)。

(2)量を示す
複数の点や線の大きさを変化させることで、量の大小が表される。図4.4に示した人の顔の図は、点の大きさで濃度(濃さの大小)を表している。また格子の移動量に対応させると、線の交差したネットの中に形がイメージされる(図4.5)。

(3)輪郭を示す
点を連続させることで輪郭を示すことができる。円状に配置された点群は、それぞれが連結し2つの線の交わりのように見える(図4.6)。また北斗七星は、点として見える星の間に線があるものとして見ていることを示す例である(図4,7)。

(4)勾配を表す
線や点の密度が変化することによって面の勾配が知覚される(図4.8、図4.9)

(5)領域を表す
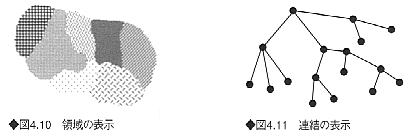
点や線の密度や並び方を変化させ、領域を区別して表すことができる(図4.10)
(6)連結を示す
点を連結することにより、主従関係やネットワークが示される(図4.11)。
(7)記号を示す
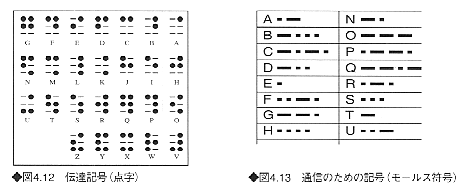
点や線の組合せで特定の記号を表す。点字は縦3行横2列の凸状の点の組合せからなる64の符号を基本とし、これによりアルファベット、数字など各種の記号が作られている(図4.12)。また、モールス符号は長符(線)と短符(点)の組合せによってこれらを表している(図4.13)。
《2》線の作り出す造形
(1)いろいろな曲線
ここでは、造形要素としてのさまざまな曲線の定義、およびその描き方について述べる。
〈円(circle)〉
円は、中心からの距離が一定の点の軌跡である。
原点を中心とする円をコンピュータで描く場合、動点P(x,y)は、中心からの距離をrとすれば、

で表されるので、tの増分を細かくとれば滑らかな円を描くことができる。
〈螺旋(spiral)〉
回転角の増加にしたがって、中心からある一定の割合で動径(中心と動点の距離)が増加していくものを螺旋という。
アルキメデスの螺旋(Archimedean spiral)は、回転角に正比例して動径が等差数列的に増加するもので、極座標(r,t)を用いてr=at(aは任意の値)で表される。
対数螺旋(logarithmic spiral)では、r=r0at(r0は最初の動径)のように、角度θの増加に従って動径が等比数列的に変化する。
〈サイクロイド(cycloid)・トロコイド(trochoid)〉
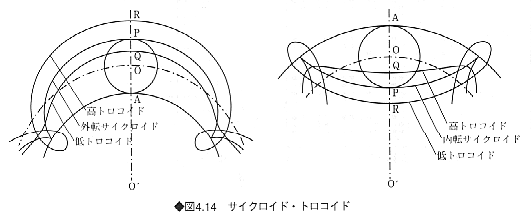
円に接しながら転がる別の円(転円)の円周上の点Pの軌跡は、サイクロイドとよばれる。また、点Pが円周上ではなく半径上にあるときは低トロコイド、半径の延長上にあるときは高トロコイドとよばれ、サイクロイドとは異なった曲線となる(図4.14)。さらに、円(導円という)の外側を転円が転がる場合(外転)と、内側を転がる場合(内転)との区別も考えられる。
サイクロイドは、極座標(r,t)によってr=a(1+cos t)で表される。
内転サイクロイドのうち、転円と導円との直径が等しい場合(a=1)をカージオイド(cardioid)という。また、転円の直径が導円の直径の1/4のときアステロイド(asteroid)となる。
〈花形の曲線〉
極座標(r,t)で、r=cos(m/n)t+aとし、m、n、aにいろいろの値を与えると、花やヒトデの形の曲線が得られる。
<リサージュ曲線(Lissajous's curve)〉
原点を中心とする円を媒介変数を用いて表すと、

となる(rは円の半径)。
このとき、

のようにして、m、nにさまざまな値を与えると、いろいろなリサージュ曲線が描ける(2-4-3参照)。リサージュ曲線などを利用した作品例を図4.15、図4.16に示す。


(2)曲線を使った造形
ラポスキー(Ben F.Laposky)は、1950年代初頭に、波形発生器とオシロスコープおよび記録用のカメラからなるOsillonという装置を制作し(図4.17)、陰極線アート作品を発表している(図4.18)。


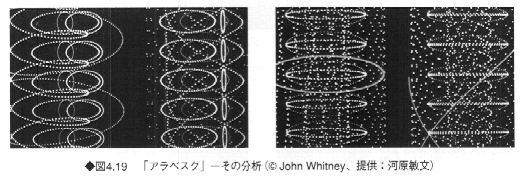
コンピュータアートの父ともいわれるホイットニー(John Whitney)は、1968年の「アラベスク(Arabesuque)」や「パーミュテーション(Permutation)」といった作品のなかで、点群によって構成されたリサージュパターンの周期を変化させ、右へ左へ、上へ下へとパターンを動かし、反復と収束の感覚を与える映像を制作している(図4.19)。
1973年に、ドライヤー(Ivan Dryer)は波形合成によって作られた信号によって、XY方向に直交して設置された2つのスキャナミラーを走査し、レーザー光をミラーに当ててレーザーパターンを作り出した。これは、ロサンゼルスのグリフィス天文台プラネタリウムのドームに、クリプトンレーザーによる赤、黄、緑、青の幾何学パターンを音楽とともに投影して幻想的な宇宙空間的イメージを演出したもので、このショーは「LASERIUM」と名付けられ、全米各地をはじめ日本、ヨーロッパなどでも公演された(図4.20)。

このように、造形の基本要素として曲線を基調とした映像作品は比較的多い。
 立体造形
立体造形
立体図形には、多面体、曲面、およびそれらの複合図形がなどがある。
多面体は平面のみによって構成される立体である。すべてが合同な正多角形で構成される多面体を正多面体といい、正三角形からは正四面体、正八面体、正二十面体を、正四角形からは正六面体を、正五角形からは正十二面体を作ることができる。そのほか2つ以上の正多角形から構成された多面体として、正三角形8個と正方形18個からなる二十六面体、正五角形12個と正六角形20個からなる三十二面体など13種類が知られている。
米国フロリダ州のオーランドにあるエプコットセンターのシンボルは正三角形を組み合わせた多面体からなる巨人なドームで、その造形の精繊さに驚かされる(図4.21)。

曲面は、代数曲面と自由曲面に大別できる。代数曲面はx、y、zの3変数の多項式で表現でき、球、円柱、円錐などは2次曲面として表されるが、さらに複雑な自由曲面の形状を表すためには曲面パッチが用いられる。曲面パッチを構成する長方形領域を(u,v)平面とみなし、S(u,v)のパラメータ形式で表現するパラメトリック曲面で複雑な形状の立体を表す。図4.22は2次曲面を利用した横浜博における造形の例で、金網で曲面を形成させている。

 形の法則性
形の法則性
人が美しいと感じる形には、さまざまな法則性が潜んでいることがある。ここではこうした造形 要素のいくつかをとりあげる。
《1》形と比例
比例(proportion)とは、大きさや長さの対比を表すが、われわれは、ある一定の比例関係に調 和や均衡、あるいは変化を感じ、そこに美しさを感じることがある。
(1)等差数列
互いに隣接する数と数の差がつねに等しい数列を等差数列(arithmetric progression)とよぶ。任意の長さを1倍、2倍、3倍、4倍、5倍、......のように、その間隔を等しくとると等差数列が得られる。この数列は変化に乏しく単調であるが、安定さを感じさせることもある。
(2)等比数列
2、4、8、16、32、64、......のように、隣接する数と数との比が一定の数列が等比数列(geometric progression)である。これは変化のある数列ということができる。
(3)調和数列
1、1/2、1/3、1/4、......のように、等差数列の逆数による数列は調和数列(harmonic progression)とよばれ、比較的変化のある美しい数列が得られる。
(4)フィボナッチ数列
1、1、2、3、5、8、13、21、34、55、89、144、233、......のように、直前の数とその前の数を足した値が次の数になるような数列をフィボナッチ数列(Fibonacci
series)とよぶ。この数列の隣接する2つの数の比は、極限において(1+√5)/2=1.61......の黄金比に近づく。
なお、黄金比は2つの数a、bが、a:b=b:a+bの関係にあることを意味する。
(5)ペル数列
1、2、5、12、29、......のように、直前の数を2倍にしその前の数値を加えるとペル数列(Pell series)となる。極限において、隣接する2つの数の比がθ=1+√2=2.4142......となる。この数列には美的な変化がみられる。
(6)ルート矩形
ルート矩形(root rectangle)は辺の比が1:√xの関係にある矩形をいう。1:√2の矩形を√2矩形とよび、古代ギリシアから理想的比例と考えられ構成の基本となった。さらに√2矩形の対角線は√3となる。√3矩形の対角線は√4となり、√4矩形の対角線は√5となり、同様に対角線を求めていくと√n伍矩形が得られる。
ル・コルビジェは、自身のデザイン用の尺度をモデュロール(le modulor)と名付けた。これは黄金比を基本とし、人の身体的な寸法とも対応させたものである。人が手を上げたとき、手先から頭頂まで、頭頂からへそまで、へそからかかとまでに区分すると相互の関係に黄金比を含んでおり、フィボナッチ数列を基本とした比率となっているルート矩形や黄金比にみられる比例関係は、東西に共通の美的な基準として、また自然界の形態のなかに見いだすことことができる。
《2》秩序づけられた形
スペインのグラナダにあるアルハンブラ宮殿の装飾に用いられているアラビア模様は非常に複雑に見える。しかしこれらの模様をよく見てみると、単純なユニットの回転や平行移動などによってパターンが構成されていることがわかる(図4.23)。さらに、そのなかには対称性という要素も見られ、こうした模様の規則性や、そのなかに現れる変化が我々の美的感覚に訴えるのである。

《3》平面充填パターン
合同な図形で平面を覆いつくす連続パターンは、しばしば装飾パターンとして用いられる。連続パターンを作り出す図形としては、三角形、四角形、正六角形などがあげられる。そのほかに、凸六角形と凸五角形も、ある条件では平面を埋め尽くすことができることがわかっている。
これらの平面充填パターンは、鏡映や回転などとも複合して構成される。こうしてできた平面充填パターンは、図形生成の手続きとして行った方法が、そのまま図形を見るときの見え方とは必ずしもならない。見る側においては、隣接したパターンとの図形的な結合や視覚的な連続性によって、生成ルールの段階では予測できないような形として認識されることもある(図4.24)。

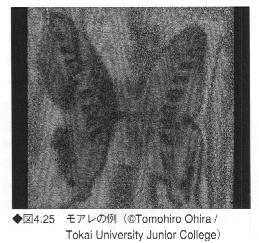
《4》モアレ
ほぼ同じ周期的構造をもったパターンが重なり合ったときに生じる別のパターンをモアレという。平行線のパターンや、点が等間隔に並んだパターンを使い、原パターンの上に同一のパターンをわずかに角度をずらして重ね合わせると、新たな二次的パターンが発生する(図4.25)。重ね合わせる2つのパターンは同一のパターンでなくてもよく、周期的な構造が類似していればモアレが生成される。
《5》オプティカルパターン
モアレや平面充填パターンは、人間の視覚刺激に訴えるものが多く、時として実際には存在しない色(主観色)が感じられることもある。1960年代には、これらの視覚刺激や錯視などの知覚現象を意識した芸術が生まれ、オップ・アート(op
art:optical art)とよばれた。オップ・アートは、1965年にニューヨーク近代美術館で開催された「感応する眼(The Responsive
Eye)展」に集約される。さらにこの流れを受け継ぎながら、当時の最新のテクノロジーの成果であるコンピュータと感覚の問題とを結合し、初期の多くのコンピュータアートの作品が生まれた。「Cybernetic
Serendipity」は、1969年に当時のコンピュータアートの集大成としてロンドンの現代芸術研究所で開催されたものである。1970年後半から80年代のリアリスティックな表現を中心としたCGが社会的に注目される以前に、ホイットニーやノールトン(Kenneth
Knowlton)、スーリ(Charles Csuri)、ノル(A.Michael Noll)、日本のCTG(Computer Technique Group)らは、コンピュータや出力装置の表現能力が乏しい時代に、コンピュータをすでに創造の重要な道具として自己の制作活動のなかに位置づけていたのである。
《6》分岐・自己相似形
局所的な生成ルールの繰り返しによって全体の形状が表されているものの1つとして、分岐によるパターンがあげられる。たとえば樹木は、成長にしたがって分岐し次の枝を発生させていく。図4.26に示した木の図形は、
(1)もとの枝の長さに対しある割合になったときに2本の枝を発生する
(2)2つの分岐した枝はもとの枝に対し一定の角度をもって成長するという操作を繰り返して作られたものである。このとき、分岐する前の枝に対する長さの割合、分岐の数、枝の角度、繰り返しの回数などを変化させると、さまざまな形の樹木が生成される。分岐構造は、樹木のほかにも葉脈、川の流れ、放電、神経系、ひび割れなど、自然界に多く見ることができる。

自己相似とは、ある図形の部分が全体の図形に相似な縮小図形を含んでいる性質をいい、この性質をもつ図形をフラクタル図形という。自己相似形の例としてコッホ曲線やドラゴン曲線などがあり、基本単位であるジェネレータを再帰的に用いながら生成していく。
これらの図形は、生成のための方法が指定されており、自動的にパターンを作り出す「手続き型」の図形である。誰がやっても同じ結果を得ることのできるタイプの造形である。
フラクタルについては、次節で詳しく述べる。

フラクタル理論は、マンデルブロ(B.B.Mandelbrot)によって作り出されたもので、フラクタル(fractal)という言葉は彼による造語である。自然界には、山や植物など、フラクタル性をもつものが数多く見られ、逆にコンピュータ内部でフラクタルを生成することにより、山や植物のCG画像を作ることができる。本節では、そうしたフラクタルのさまざまな性質について考える。
 フラクタルとは一自然界のフラクタルー
フラクタルとは一自然界のフラクタルー
《1》フラクタル図形
フラクタル図形の特徴である自己相似性は、全体の形状がその形状の各部分にも現れる、つまり自分自身の縮小変換の集合で表せるような形状のもつ性質をさしている。図4.27に示すコッホ曲線では、中央部を正三角形に突出させた線分がいたるところで見られ、全体形状の縮小されたものが集まって全体を構成しているのがわかる。この例のようなフラクタル図形では、どこを拡大しても同じ形状が繰り返し得られる。このような縮尺(スケール)の違いに左右されない不変性をスケーリング則といい、フラクタルの重要な特性の1つとされている。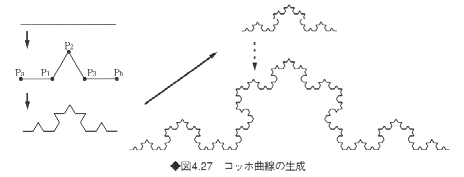
《2》フラクタル次元
フラクタル次元とは、フラクタルの特性を表す数値であり、物体の形状の複雑さを表す尺度としても用いられる。フラクタル次元が大きいほど、対象形状は入り組んだものとなっており、この値は、われわれが慣れ親しんでいる2次元、3次元といった整数値ではなく、1.28次元とか2.75次元といった非整数値をもつものである。
いま、対象図形が相似比rのN個の部分(セグメント)から構成されているものと仮定する。このとき、次の式を満たすDをフラクタル次元とよぶ。
 この式を用いて、前出のコッホ曲線のフラクタル次元を求めてみると、相似比が1/3の4個のセグメント(線分)から構成されているから、式(4.4)より(1/3)×41/D=1、すなわち41/D=3となる。両辺の対数をとって、(1/D)log4:log3から、フラクタル次元Dはlog4/log3=1.26となる。
この式を用いて、前出のコッホ曲線のフラクタル次元を求めてみると、相似比が1/3の4個のセグメント(線分)から構成されているから、式(4.4)より(1/3)×41/D=1、すなわち41/D=3となる。両辺の対数をとって、(1/D)log4:log3から、フラクタル次元Dはlog4/log3=1.26となる。
《3》フラクタル的な物体・現象
フラクタル的な性質をもつ形状・現象は、自然界に数多く見ることができる。海岸線を例にとると、地図帳の縮尺で見るような不規則で複雑な海岸線の形が、実際に海岸を見渡した範囲でも見られるし、さらに近づくと、海岸を形づくっている岩石も同じような複雑さの形状をもっている。リアス式海岸はゴツゴツした岩肌が露出しているし、なだらかな海岸の砂浜はサラサラした細かい砂粒で覆われている。これと同じ現象は、山岳の形状にも見られる。また、カリフラワーを手にとってちぎっていくと、小さなカリフラワーが次々と現われ、自己相似的な構造になっていることがわかる。さらに、人の気管支の構造や、河川の枝分かれ、樹木の枝葉の付き具合いも、同じ分岐現象の例としてあげることができる。このほか、巻貝などの螺旋構造も、フラクタル的な自己相似性をもつ例の1つである(図4.28)。

一方、フラクタル的な成長をする現象を、DLA(Diffusion Limited Aggregation)とよばれるモデルでシミュレーションすることもできる(図4.29)。
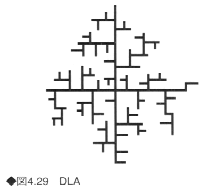
このモデルでは、ブラウン運動に代表されるランダムウォークによる凝集をシミュレートし、たとえば、電解液の中で成長する金属の析出物のパターンなどを作成することができる。
ここであげた例のほかにも、株価の変動や乱流現象、星団など、われわれの周囲にはたくさんのフラクタル的な構造をもつものが存在する。
 CGにおけるフラクタル
CGにおけるフラクタル
《1》フラクタル図形と生成文法
自己相似構造をもつフラクタル図形を生成するために、ある初期形状を再帰的に分割して求める方法がある。以下に述べるような生成文法を用いると、これを比較的簡単に行うことができる。
簡単な例として、
初期状態:b
生成規則:a→a b、b→a
の生成文法を考えよう。この場合、初期状態の文字bはこの生成規則に従い、順次b→a→a b→a b a→a b a a b→......といった文字列へと変化し、生成される文字列が自己相似になっている。このような生成文法を用いてフラクタル図形を描いてみる。文字列だけでは図形にならないので、これに線分の長さや折り曲げの角度などの幾何情報を付加して、タートルグラフィックスを用いて描画する。以下の例で用いている各記号は、それぞれ次のような意味をもつ。
F:ペンを下ろした状態で、一定距離だけ前進
+:進行方向の右側に一定角度θだけ方向転換
-:進行方向の左側に一定角度θだけ方向転換
[:現在のタートルの状態をスタックに積む
]:現在のタートルの状態をスタックからとる
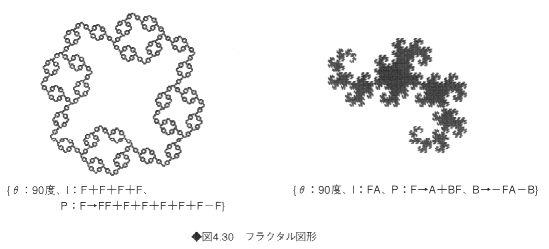
これらの記号をもとに、初期状態Iと生成規則Pを定義する。そして生成された文字列に従って、タートル・グラフィクスを用いて描画する。たとえば図4.27のコッホ曲線は以下の生成文法を用いて生成される。
θ:60度、I:F、P:F→F-F++F-F
図4.30に、このような生成規則と、それによって生成されるフラクタル図形の例をあげておく。
《2》マンデルブロ集合・ジュリア集合
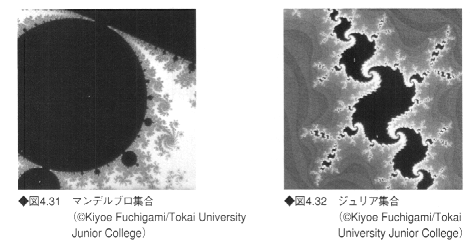
マンデルブロ集合、ジュリア集合の両集合とも、その発生源は、次の式で与えられる複素数Znの漸化式である。

式(4.5)でZ0=0とし、n→∞においてZn→∞にならないようなCの値の集合がマンデルブロ集合(図4.31)であり、Cを固定し、n→∞においてZn→∞にならないような初期値Z0の集合がジュリア集合(図4.32)である。これらの画像を作るには、単純に複素数の漸化式を、マンデルブロ集合もしくはジュリア集合の条件を満たす間繰り返し求め、その繰り返しの数に応じて色付けをすればよい。
《3》IFS
IFS(Iterated Function System:反復関数システム)手法は、ある画像をその縮小コピーの貼り合わせで近似していく手法である。この手法は、式(4.6)で表される縮小変換wの組合せで表現される。

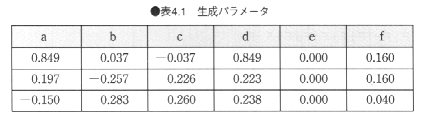
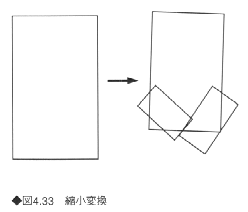
たとえば、ある長方形を表4.1に示す各パラメータでそれぞれ図4.33のように縮小変換し、変換後の各図形に対して、また同じ縮小変換することを繰り返して生成することにより、図4.34のような図形が得られる。
また、この逆変換として、与えられた画像から、表4.1に示されるようなパラメータを求めて画像を符号化する手法も提案されている。

《4》fBmと中点変位法
フラクタル理論による架空の地形の作成に用いられたのが、fBm(fractional Brownian motion:フラクタル・ブラウン運動)とよばれる、フラクタル次元をパラメータにもつブラウン運動の拡張モデルである。この手法では、山岳の垂直断面の形状をfBmによる起伏で表現しており、フラクタル次元を変化させることによって、さまざまな起伏の山岳を表現することができる。
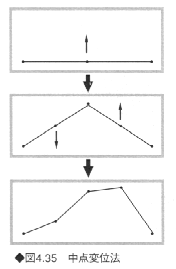
一方、fBm手法よりも計算効率がよく汎用性のある中点変位法という手法が提案された。この手法は、図4.35に示すように、与えられた線分の中点を乱数で上下に変位させる操作を繰り返すものである。
《5》1/fノイズ
1/fノイズとは、そのノイズのパワースペクトルが周波数fの逆数に比例しているようなノイズをさす。1/fノイズはホワイトノイズ(白色雑音)とはまったく性格の異なるもので、生体のゆらぎにマッチしたノイズともいえる。たとえば、小川のせせらぎ、音楽、脳波なども1/fノイズになっていることが知られている。フラクタル的な構造をもつ現象のスペクトル分布を調べると、1/fノイズになっていることが多い。
 自然物体の表現
自然物体の表現
《1》地形
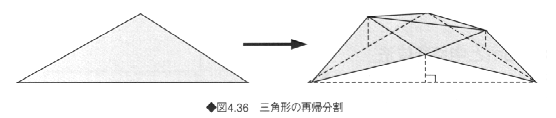
山岳などの地形を表現するには、fBmや1/fノイズを格子点に高度として与える方法や、大まかな3次元形状を三角形パッチで与え、各三角形を図4.36に示すような中点変位法を用いて再帰分割する手法などがある。図4.37に、中点変位法を用いて生成した山岳形状の例を示す。これらの手法により、未知の惑星の地表を作成したりすることも可能であり、実際にSF映画にも、牛成されたCG画像が一部取り込まれた例(「スタートレック2」など)がある。

《2》植物
植物を表現するには、植物の枝ぶりや葉の付き方をうまく表現しなければならない。植物のもつ構造的な特徴をモデル化した例として、植物学者リンデンメイヤー(A.Lindenmayer)が提唱したLシステムがある。Lシステムとは、植物の成長を記述した生成文法であり、これに枝の長さ、分枝の角度などの幾何情報を付加することにより植物を生成するものである。生成文法については「4-2-2
CGにおけるフラクタル」で述べたとおりであり、これを3次元に拡張することにより、実際の植物らしい形状を表現することができる。最近の研究例では、開花の順序や実の付き方までシミュレートすることもできる。
このようにして生成された植物は、都市計画のデザインのみならず、熱帯雨林の将来像の検証などの、植物の成長過程をシミュレーションする目的でも使用されはじめている。
《3》雲などのガス状物体
雲のようなガス状のもやもやした物体を表現するには、その物体が固体でないために、面の集合で表現することはできない。そこで、ガス状物体を構成する微粒子(雲の場合は水蒸気)の分布状態を作り出し、光の透過・減衰を計算して表現することになる。この考え方を用いて、たとえば、山岳形状の高さ情報を水蒸気の量とみなして、雲を表現することもできる。この手法により表現された雲の例を図4.38に示す。ただしこの手法では、複雑な動きのある煙などの流れを表現するには不十分なので、そうしたものの表現には、たとえば乱流現象の物理方程式を解く必要がある。

《4》テクスチャ
岩石や木目など、物体の模様や凹凸の状態といったテクスチャの生成にも、フラクタル手法は用いられている。
岩石の表面の凹凸状態は、地形の生成と同じ手法で生成することが可能であり、その岩石をさらに複雑に組み合わせることにより、図4.39に示すような石垣を作り上げることができる。木目の場合は、同心円状に年輪を生成させ、中点変位法を用いてその年輪を歪ませる。そして、年輪からの距離で色づけを行うと、図4.40に示される木目調のテクスチャが生成される。
以上の例は2次元的なテクスチャの例であったが、物体の切口などでの模様の連続性を考えた場合は、ソリッドテクスチャ(ボリュームテクスチャ)が必要である。ソリッドテクスチャでは、3次元空間内にテクスチャを発生させるため、木材の断面や、大理石のテーブルなどを表現する際の、模様の不連続性の問題は解決される。これらのテクスチャでは、フラクタル手法が大理石の揺らいだ縞模様を作る場合に用いられている(「5-5-5ソリッドテクスチャリング」参照)。

本節では、立体の内部表現法について、そのモデルの種類と特徴、およびモデルの入力と生成法について解説する。
 立体の表現法
立体の表現法
ここでは、コンピュータ内部で立体を表現するためのモデルとして、ワイヤフレームモデル、サーフェスモデル、ソリッドモデルを取り上げる。コンピュータによるモデルとは別に、実際に粘土、木、石膏などによって作られるものをクレイモデルという。
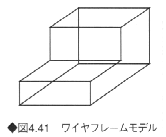
《1》ワイヤフレームモデル
ワイヤフレームは、立体の骨組み構造だけを直線や曲線で表現したモデルである(図4.41)。立体の面の表示や立体どうしの衝突チェックなど、物が詰まった立体としての処理はできない。たとえば立体の面のレンダリングなどはできない。立体の移動・表示などをリアルタイムに行う場合や、建築物など直線要素の多い立体を表現して高速に表示したりするのに向いている。
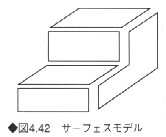
《2》サーフェースモデル
立体の面データだけを表現したモデルで、面の隠線消去表示や面のレンダリングが行える(図4,42)。面の形状が重要な意味をもつ場合によく利用される。
《3》ソリッドモデル
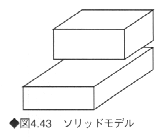
実物と同じように、物が詰まった立体としての完全な立体データを表現したものである(図4.43)。レンダリングや稜線表示などの各種表示が可能で、集合演算を行って和・差・積の複合形状を生成したり、さまざまなシミュレーションが行える。他の表現方法と比較すると、データの生成や処理に多量の時間を必要とする。
 表現法の種類
表現法の種類
立体モデルのより具体的な表現方法として、境界表現、CSG表現、ボクセル、オクトリー、スイープ表現がある。さまざまな形状をコンピュータの限られたメモリで効率よく表すために、こうしたいろいろな方法が必要となる。
《1》境界表現
境界表現はB-repまたはB-reps(boundary representation)ともいわれる。多面体などの立体は頂点、稜線、面から構成されているが、これら頂点、稜線、面のデータを数値によって表し、また、それらの関係を接続グラフで示すことにより立体を表現する考え方が境界表現である(図4.44)。
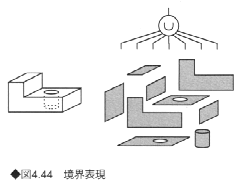
はじめに立体は面から構成されていると考える。四角形やL字型の面もあれば、穴の開いた面もある。また円柱面などの曲面もあり、システムによっては曲面を複数の平面で近似する場合もある。
面の形状は面の方程式と境界線から構成される。境界線は稜線に相当し、稜線の端点が頂点となる。
このように、立体のデータには頂点の座標や面の法線ベクトルなどの幾何学的情報と、頂点、稜線、面の結合などの接続関係情報がある。頂点、稜線、面で構成できれば任意形状が表現できる。
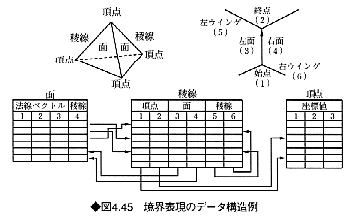
境界表現のデータ構造の例を図4.45に示す。面、稜線、頂点などのデータを格納する配列変数がある。頂点データとしては頂点座標のx、y、z成分がそれぞれ数値として蓄えられる。稜線のデータは、1つの稜線に注目した場合の頂点・稜線・面の結合状態を示している。ここに記録される数値は、たとえば頂点データ配列の要素番号である。これを参照することにより、始点・終点の頂点の要素番号、左右の面の要素番号がわかり、頂点や面データを取り出すことができる。面データには、面の法線ベクトルのx、y、z成分、面を囲む1つの稜線の番号などのデータがある。
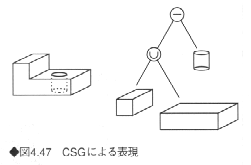
《2》CSG表現
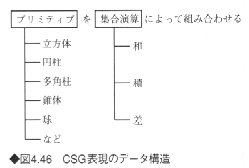
CSGとはConstructive Solid Geometryの略で、立体を基本立体(プリミティブ)とその組合せで表現する。図4.46のように、基本立体の種類、大きさ、位置の情報とそれらの結合状態(和、差、積のどの結合で組み合わされるか)をツリー構造にしておく。基本立体には立方体、円柱、多角柱、錐体、球などがあるが、境界表現と違って任意形状は表現しにくいので、いろいろな基本立体を用意しておく必要がある。
図4.47がCSGによる表現の例である。この立体は図4.44と同じもので、L字型のブロックに円柱状の穴が開いている。したがってこれをCSGで表すには、L字状の立体を2つの直方体の和結合として定義し、これから円柱状の立体を引き算すればよい。
《3》メタボール
すべての立体を球の集合体で表すのがメタボールで、グラフィックスの分野ではよく使われる方法である。メタボールは点が及ぼす影響力(引力)の和が一定値となるような点によって形成される曲面である。複数のボールがあるときは、これらを包むゴムの幕のような曲面となる(図4.48)。
複雑な曲面形状を表現する場合に、自由曲面を用いずにメタボールの集合体として表すことができる。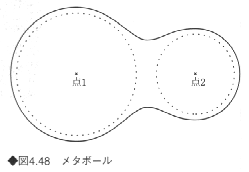
《4》ボクセル表現
ディスプレイに表示された図形は一般に格子点上に配置した小正方形(画素)の集合で表される。 この方法と同じように、立体を3次元の格子点上の小立方体の集合で表すのがボクセル表現である(図4.49)。2次元の小正方形を画素(ピクセル:pixel)とよぶのに対し、3次元の小立方体をボクセル(voxel)という。境界表現やCSGと比較すると、データ量が膨大で精度が劣り、立体の表示・移動・回転などは手間がかかるという問題がある。
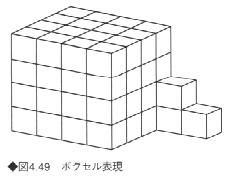
しかし、データ構造が簡単で、集合演算がきわめて簡単な原理で行える。人工的で規則的なものでなく、自然界にある非常に不規則な形状を表す場合に向いている。
《5》八分木(オクトリー)
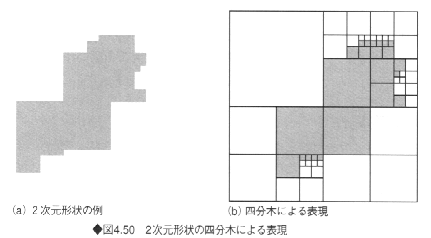
ピクセルの集合の2次元図形を表す手法に四分木(quad-tree)がある。図4.50のように、平面全体をそれぞれ縦横半分に分割すると4つの領域に分割される。各領域がすべて図形に占められているか、あるいは図形がまったく含まれない場合は分割を中止し、それ以外の場合はその領域をさらに4つの領域に分割していく。このような再帰的手法によりすべての平面図形は四分木のツリー構造で表現できる。図形の形状にもよるが、四分木表現により、ピクセル表現よりデータ量を縮小させることができる。
四分木表現を3次元のボクセル表現に対応させたのが八分木(オクトリー:oct-treeまたはoctree)である。2次元の場合、x、y座標をそれぞれ分割すると4つの領域に分かれる。3次元の場合はx、y、z座標をそれぞれ分割すると8つの領域に分割される。オクトリーの形で表現することにより、ボクセル表現よりデータ量を縮小することができるので、ボクセルを改良した表現法ということができる。
断面をとる位置を少しずつずらして得た複数のCT画像によって得られる、きわめて複雑な形状の立体に、ボクセル表現やオクトリーがよく用いられる。
《6》スイープ表現
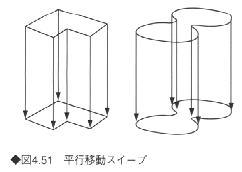
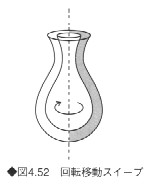
スイープは、ある平面図形を一定方向に移動するときの軌跡によってできる立体である。モデリングの対象とする形状にはスイープで表せる形状が多く、さらにスイープを組み合わせてさまざまな形状を表現することができる。よく使われるスイープとしては、平行移動スイープ(図4.51)と、回転移動スイープ(図4.52)がある。
 立体の演算
立体の演算
《1》立体の生成
われわれの身の周りには、建物、家具、電化製品、自動車など、人工的に作られたものが豊富にある。これらのものには回転体、面対称立体、スイープ形状など、形状に規則性のある立体が多い。これらの形状を容易に生成するために、その形状を構成する面を作る処理を自動化することが広く行われている。
回転体は、ある平面図形を回転したときにできる立体である。平面図形が多角形のとき、平面図形を構成する線分と回転軸との位置関係によりいろいろな面が生成される。回転軸に平行な線分に対しては円柱面が生成される。また回転軸に垂直な線分は回転すると平面(円形の平面)になる。これ以外の一般の線分は円錐面となる。
鏡像コピーは、面対称の立体を生成する場合に、半分だけのデータを生成して、残りを自動的に生成する方法である。立体のデータをそのままコピーして、これに面対称変換を施せば鏡像立体ができる。ただし、対称面において2つの立体を接続するための処理が必要になる。
スイープでは、平面図形とスイープ方向のベクトルを与えて自動的に生成するのが普通である。
境界表現の場合も、生成規則を考えれば、自動的に立体を生成することができる。
《2》局所変形操作
局所変形操作はオイラー操作ともよばれ、境界表現の立体に対し、頂点、稜線、面などの位置や接続構造を入力したり修正したりする方法である。たとえば、直方体の1つの面を2つに分割し、一方の面を平行に持ち上げてL字型の立体を生成するような操作である。この作業は対話的に行うことが多い。たとえば、ディスプレイに立体を表示し、マウスで入力点や対象の場所、修正箇所、修正方法などを入力する。
多面体の頂点、稜線、面を移動する場合に、たとえば四角形の1頂点だけを移動すると、平面四角形でなくなってしまうことがあるため、ほかのいくつかの頂点も同時に動くようにしておく必要がある。また、対話的な作業では、入力ミスや、やり直しなどのことを考え、途中の結果を随時保存しておくよう心がける必要がある。
《3》集合演算
複数の立体を組み合わせて複合形状を生成するのが集合演算である。集合演算には、和、差、積の3種類がある(図4.53)。
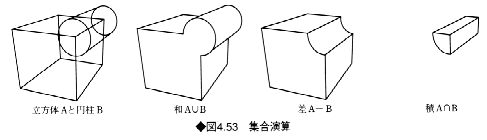
和の集合演算は、2つの立体が結合した形状を生成する。言い換えると、どちらか一方、あるいは両方の立体が存在する領域を示す。
差の集合演算は、2つの立体の一方からもう一方を引き抜いた形状を生成する。2つの立体をA、Bとすると、A-BとB-Aの2種類がある。
積の集合演算は、2つの立体の共通部分、すなわち、2つの立体が同時に存在する領域を表す。
A、Bの積集合はド・モルガンの法則により、Aの補集合とBの補集合の和集合の補集合となる。立体の補集合は反転とよばれ、境界表現の場合は面の表と裏を入れ替えることにより表現できる。
したがって、積の集合演算処理は、反転操作と和の処理を利用して行われる。同じように差の集合演算も反転操作と和の演算から生成することができる。
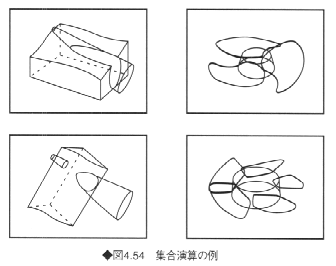
図4.54は、複数の立体の和や差による集合演算の結果を示したものである。立体はすべて境界表現で表され、隠線消去はしていない。いずれも自由曲面を含む立体どうしの集合演算である。
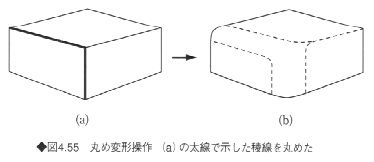
《4》丸め変形操作
立体の頂点や稜線などで角を取って丸める操作で、局所変形操作の一種であるが、しばしば使われる操作であるため、別の機能として用意しているCADシステムも多い(図4.55)。

本節では、CGにおいて利用される曲線と曲面の表現法と利用法について解説する。
 曲線・曲面の分類とCGへの応用
曲線・曲面の分類とCGへの応用
ここでは、まず曲線と曲面を表現形式の観点から分類する。その上でCGにおいてよく利用される2次曲線・曲面とパラメトリック曲線・曲面の位置付けと利用法について言及する。
CGにおいて曲線や曲面を利用する場合には、すべて数学的な表現形式を基本としている。したがって、まず数学的な表現形式、すなわち数式という観点から曲線・曲面を分類しておく必要がある。ここでは曲線と曲面を以下の3種類に分類する。
①陰関数形式(implict function form)
②パラメータ形式(parameter form)
③陽関数形式(explict function form)
《1》陰関数形式
陰関数形式は関数を陰に用いて曲線を定義する。曲線上の点は1自由度、曲面上の点は2自由度をもつ。そこで、2次元空間ないし3次元空間において、自由度を制限することにより曲線や曲面を表現する。1つの等式によって1自由度が拘束されるので、次のように、平面曲線の場合には等式1つ、空間曲線の場合には等式2つ、3次元空間内の曲面は等式1つによって表現される。
平面曲線f(x,y)=0
空間曲線f(x,y,z)=g(x,y,z)=0
曲面f(x,y,z)=0
たとえば、xy平面において原点を中心とする半径rの円は、

となり、原点を中心とする半径rの球面は、

となるが、これらは陰関数形式による表現である。 陰関数形式で表現された曲線・曲面は、表現式そのものが方程式であるだけに、交線計算などが容易に実現できる。
これは連続な関数fによって
f>0ないしf<0
となる、2つの部分に分割された空間の境界が曲線あるいは曲面になっていることに由来している。すなわち平面曲線の場合には、曲線をはさむ左右両側の点で
関数f(x,y)を評価すると、
一方は
f(x,y)>0
となり、他方は
f(x,y)〈0
となる。また曲面の場合には、曲面をはさむ両側の点で関数f(x,y,z)を評価すると、一方は
f(x,y,z)>0
となり、他方は
f(x,y,z)<0
となる。前に示した球面の場合には、球の外部の点で関数を評価するとf(x,y,z)>0、球の内部の点で関数を評価すると
f(x,y,z)〈0
となる。したがって、2分法やニュートン法などの収束計算が簡単に利用できる。たとえば、先ほどの球面と、点
p=(xp,yp,zp)
を通ってベクトル
v=(xv,yv,zv)に平行な直線p+tv
との交点は、

という、tについての2次方程式を解けば求められる。曲面表示の手法としてよく用いられるレイトレーシングでは、直線と曲面の交点計算を繰り返し行う必要がある。したがって、レイトレーシングには陰関数形式の曲面が適している。
一方で陰関数形式は、曲線や曲面上の点を適当な間隔でサンプリングするのには適していない。
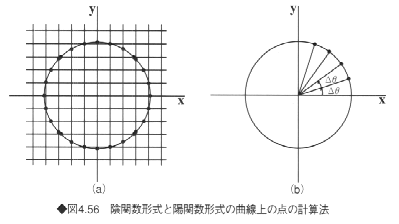
曲線の表示は曲線上の適当な点列を用いた折れ線表示、曲面の表示は曲面上での格子状の点列をもとにした折れ線表示や多面体化による陰影画表示が普通である。しかし、陰関数形式の曲線・曲面では、これらの点列の計算が、後述する陽関数形式の曲線に比べて困難である。曲線・曲面上の点列を求める必要がある場合には、直線との交点計算が容易であることから、図4.56の左のように各軸に平行な格子線との交点を求める手法が一般的である。
陰関数形式の平面曲線のうち、関数が多項式関数であるものを代数曲線(algebraic curve)とよび、陰関数形式の曲面のうち、関数が多項式関数であるものを代数曲面(algebraic
surface)とよぶ。このとき、多項式の次数nを曲線あるいは曲面の次数とよぶ。


さらに、2次の代数曲線は2次曲線(quadrics, quadric curve)ないし円錐曲線(conics)、2次の代数曲面は2次曲面(quadrics,
quadric surface)とよばれる。
《2》パラメータ形式
パラメータ形式はパラメータを用い、その陽関数として曲線・曲面を定義する方法である。すなわち、1次元実空間すなわち数直線Rから2次元空間ないし3次元空間への写像によって曲線を表現し、2次元実空間すなわち平面R2から3次元空間への写像により曲面を表現する。つまり、パラメータt∈Rについての関数として曲線を定義し、パラメータ(u,v)∈R2についての関数として曲面を定義する。

たとえば、xy平面において原点を中心とする半径rの円は、

となり、原点を中心とする半径rの球面は、
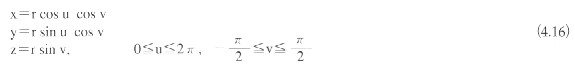
となるが、これらはパラメータ形式による表現である。
パラメータ形式の曲線ないし曲面は、パラメトリック曲線やパラメトリック曲面ともよばれる。 パラメトリック曲線・曲面は、CGで非常によく用いられる曲線・曲面である。これはこの形式の曲線・曲面の場合に、曲線・曲面上の点列を求めることが非常に容易であることに由来している。曲線の場合にはti+1=ti+△tとなるパラメータ値ti、曲面の場合にはui+1=ui+△u、vj+1=vj十△vとなるようなパラメータ値の組(ui,vj)をくり返し代入評価することによって、図4.56(b)のように各パラメータ値に対応した曲線ないし曲面上の点列が得られる。したがって、曲線や曲面の折れ線表示や曲面の多面体表示が簡単にできるという特徴がある。
一方、交点計算は陰関数形式ほど容易ではない。たとえば、原点を中心として半径rの球面と、点p=(xp,yp,zp)を通ってベクトルv=(xv,yv,zv)に平行な直線p+tvとの交点は、

という、3元連立方程式を解かなくてはならない。これは本来まったく同じ内容の(4.9)式に比べて、非常に解きにくい式になっている。つまり、パラメータ形式の曲面はレイトレーシングには向いていない。
《3》陽関数曲線・曲面
陽関数曲線・曲面は、陰関数形式ともパラメータ形式ともとれる表現形式で、1つの関数によって曲線・曲面が定義されるものである。陽関数曲線の表現対象は平面曲線に限られる。

たとえば、2次関数の曲線

は関数曲線であるが、

と書けば陰関数形式とみなせるし、

と書けばパラメータ形式とみなせる。陽関数曲線では任意のX座標に対して曲線上の点がたかだか1つ存在する。
次に陽関数曲面の例をあげよう。回転放物面

は陽関数曲面であるが、

と書けば陰関数形式とみなせるし、 
と書けばパラメータ形式とみなせる。陽関数曲面の場合、任意のxy座標の組に対して曲面上の点がたかだか1つ存在する。
 2次曲線
2次曲線
2次曲線は2次多項式によって表現される代数曲線であり、楕円(ellipse)、放物線(parabola)、双曲線(hyperbola)の3種類に分類される。2次曲線は円錐曲線ともよばれるが、これはすべての2次曲線が円錐面の断面線として得られることに由来している(図4.57)。断面をとる平面が円錐面の母線よりも深い角度で軸に交わる場合は楕円となる(同図(a)(e))。とくに平面が円錐面の軸に垂直の場合は円となるが(同図(d))、円は楕円の特別な場合とみなされる。また、平面が円錐面の母線に平行となる場合は放物線となり(同図(b))、平面が母線よりも浅い角度で軸に交わる場合は双曲線となる(同図(c)(f))。当然のことながら、2次曲線は平面曲線である。
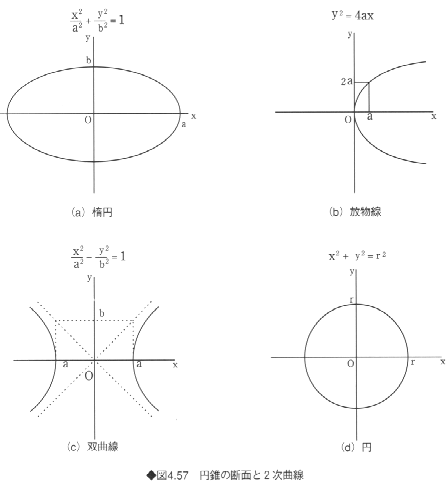
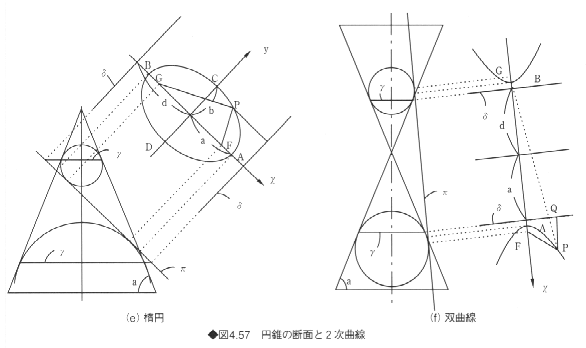
2次曲線は、平面上の平行移動と回転によって、次に示す標準座標系に変換できる。標準座標系における2次曲線の表現式は以下のようになる。
①楕円
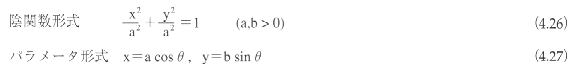
②放物線  ③双曲線
③双曲線 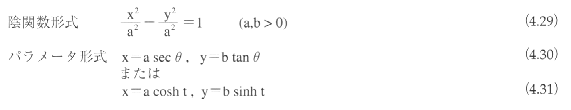
超2次曲線
超2次曲線(superconics)は一般的に用いられる曲線ではないし、用語自体もそれほど一般的ではない。しかし、よく用いられる超2次曲面(superquadrics)について学ぶために、ここで超2次曲線について説明しておく。
超2次曲線は2次曲線を拡張して、丸みを制御できるようにしたものである。超2次曲線には、超楕円(superellipse)と超双曲線(superhyperbola)がある。
超2次曲線も、平面上の平行移動と回転によって標準座標系に変換できる。標準座標系における超2次曲線の表現式は以下のようになる。
①超楕円
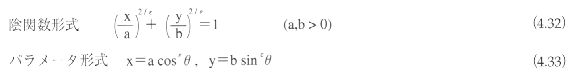
②超双曲線 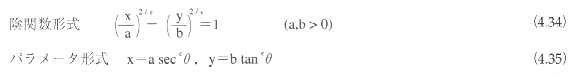
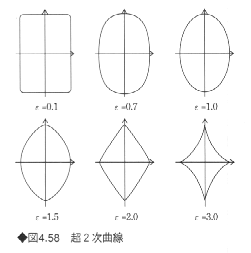
ここでε∈(0,∞)が丸めの制御パラメータである。ε=1のとき、通常の2次曲線になる。図4.58からもわかるように、εの値に応じて、形状は以下のようになる。

 パラメトリック曲線
パラメトリック曲線
パラメトリック曲線はパラメータの陽関数形式で表現された曲線である。このときの関数が多項式関数である場合には多項式曲線(polynomial curve)とよばれ、有理式関数である場合には有理式曲線ないし有理曲線(rationalcuwe)とよばれる。前項では2次曲線のパラメータ形式として三角関数を用いた表現を示した。2次曲線も多項式や有理式のパラメトリック曲線として表現できる。たとえば放物線の場合には、

というように多項式曲線となる。一方、楕円の場合には、
双曲線の場合には、

というように有理式曲線になる。このように代数曲線としては同じ2次曲線に分類されるが、放物線は多項式曲線となり、楕円と双曲線は有理式曲線となる。
一般にパラメトリック曲線では、適当なパラメータ区間に対応する曲線部分のみを利用し、曲線全体を扱うことはまれである。この曲線部分のことをセグメント(segment)とよぶ。複雑な曲線形状を扱う場合には、複数のセグメントをつなぎ合わせて1本の曲線を表現する。このように複数の曲線を合わせて1本の曲線を表す手法を複合曲線(composite
curve)とよぶ。また各セグメントが多項式曲線であれば区分多項式曲線(piecewise polynomial curve)、有理式曲線であれば区分有理式曲線とよぶこともある。
CGでは、以下にあげる曲線がよく利用されている。
エルミート(Hermite)曲線
ベジェ(Bezier)曲線
有理ベジェ(rational Bezier)曲線
Bスプライン(B-spline)曲線
非一様有理Bスプライン(non uniiform rational B-Spline)曲線
《1》エルミート曲線
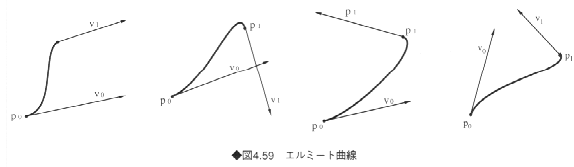
エルミート曲線は、セグメントの両端点とそこでの導関数が与えられたときに、それらを補間するものとして定義された曲線である。エルミート曲線は、通常、パラメータ区間[0,1]において定義される多項式曲線となる。CGでよく用いられるのは、多項式の次数が3次のエルミート曲線である。3次エルミート曲線は、図4.59に示すように、端点p0、p1とそこでの接ベクトルv0、v1によって定められる。表現式は以下のようになる。

ここで、H3i(t)は3次エルミート関数とよばれる多項式である(上付添字の3は、3次という次数を示している)。両端点(t=0,1)における条件から、次の性質を満たさなくてはならない。
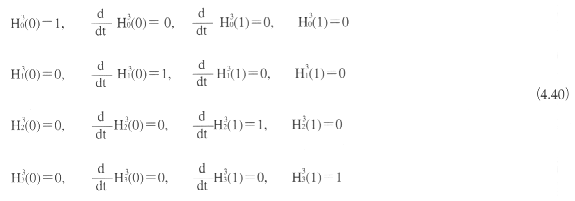
これを解くと、次のようになる。

《2》ベジェ曲線
ベジェ曲線では、制御点(control point)とよばれる複数の点piによって曲線が定義される。制御点は曲線の両端点と概形を定める。ベジェ曲線も、通常、パラメータ区間[0,1]において定義される多項式曲線で、以下の式で与えられる。

ここで、Bni(t)はn次のバーンスタイン関数とよばれ(上付添字のnは次数を示している)、次のように2通りの定義がある。
①再帰的定義

②決定的定義 
バーンスタイン関数の重要な性質として、以下の恒等式がある。

ここで式(4.42)を見ると、ベジェ曲線上の点P(t)は、制御点piの荷重平均になっている。パラメータtが変化すると、各制御点に対する重みBni(t)が連続的に変化して、点P(t)が連続的に移動する。この点の軌跡がベジェ曲線にほかならない。
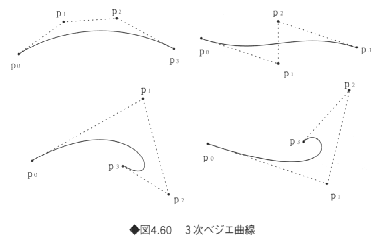
CGでは次数が3次までのベジェ曲線がよく用いられる。3次ベジェ曲線は、図4.60に示すように、4個の制御点p0、p1、p2、p3によって定められ、表現式は以下のようになる。

ただし、3次バーンスタイン関数は次のようになる。

図からわかるように、ベジェ曲線の両端点は両端の制御点に一致し、そこにおける接ベクトルは端の制御点と1つ隣の制御点を結んだ向きになる。この性質は端点一致性とよばれ、ベジェ曲線が広く用いられる理由の1つとなっている。
ベジェ曲線の性質には、このほかに以下のものがあげられる。
①凸包性
区間t∈[0,1]における曲線は、制御点の構成する凸包の内部に存在する。
②変動減少性
曲線は制御点列の形状を滑らかにした形になる。
③疑似局所制御性
制御点を移動するとその点に対応する曲線部分が大きく変形する。
④直線再現性
制御点を直線上に配すると曲線は直線になる。
⑤アフィン不変性
曲線にアフィン変換を施した結果とアフィン変換を施した制御点から得られる曲線が等しくなる。
ベジェ曲線は文字の輪郭線を数式として表現するアウトラインフォントにしばしば用いられている。たとえば、Windowsで使用するフォントを定義するTrue
Type Fontでは2次ベジェ曲線を採用し、Post Script(プリンタの制御に用いる言語)やMETAFONT(文書清書システムTeXのための文字フォント定義用言語)では3次ベジェ曲線を採用している。
3次ベジェ曲線によるアウトラインフォントの例を図4.61に示す。
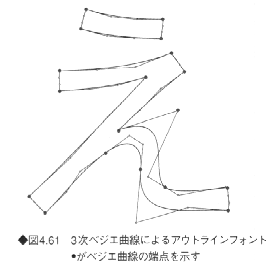
《3》有理ベジェ曲線
有理ベジェ曲線は、制御点piと各制御点に対応する重み(weight)wiによって定義した曲線である。重みとは、図4.62に示すように制御点を相対的に重みづけする値で、すべての重みが等しいとベジェ曲線と等しくなる。有理ベジェ曲線はパラメータ区間[0,1]において定義される有理式曲線で、以下の式で与えられる。
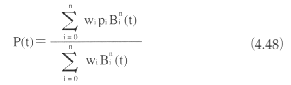
ここでBni(t)はn次のバーンスタイン関数である。
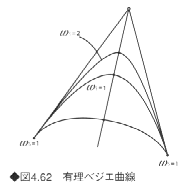
有理ベジェ曲線はベジェ曲線の性質に加えて以下の性質をもっている。
①重み
重みwiによって曲線の形をより細かく制御できる。
②2次曲線
ベジェ曲線では表現できない円や楕円、双曲線を正確に表現できる。
③射影不変性
曲線に射影変換を施した結果と射影変換を施した制御点から得られる曲線が等しくなる。
《4》Bスプライン曲線
Bスプライン曲線は、制御点piとノット列(ノットベクトル)tiによって定義された曲線である。ノット(knot)とは、曲線が定義されるパラメータ区間の境界の値である。また、ベジェ曲線ではバーンスタイン関数が用いられたが、Bスプライン曲線ではBスプライン関数を用いる。このBスプライン関数の定義にノット列が使われる。ノット列のノット値は単調増加ti≦ti+1でなくてはならない。ノット値が一定間隔ti+1=ti+△tの場合には一様(uniform)であるといい、ノット値が一致するti=ti+1の場合には多重化しているという。
n次のBスプライン関数NF(t)は次式で与えられる。
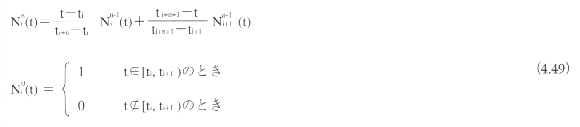
たとえば、ノット列(t0,t1,t2,t3,t4,t5)=(-2,-1,0,1,2,3)の2次Bスプライン関数は以下のようになる。

この定義からわかるように、n次のBスプライン関数はtマ[ti,ti+n+1】のときNni(t)=0となる。このような性質をもって、「Bスプライン関数は局所台をもつ」という。さらに局所台においても各区間[ti,ti+1]ごとに異なった多項式関数となる。このように区間ごとに1つの多項式として表現される関数は、区分多項式関数とよばれる。n次Bスプライン関数は、ノットが多重化していない限りCn-1級の連続性を保証し、ノットが1つ多重化するごとに連続性のクラスが1つずつ下がる。
またバーンスタイン関数はBスプライン関数の一種であることが知られている。
L個のセグメントからなるBスプライン曲線Pj(t)のj番目の区間(ただしj=0,...,L-1)は、パラメータ区間[tn,tn+L]において定義される区分多項式曲線で、以下の式で与えられる。

2つの関数f1(x)、f2(x)が、ある点x=x1で次の性質を満たすとき、この2つの関数が「Cn級の連続性をもつ」という。

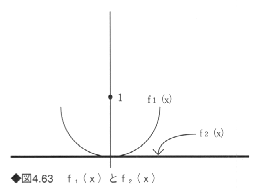
たとえば、f1=1-√1-x2とf2(x)=0は、x=0でC1級の連続性をもつ(図4.63)。
局所台の性質から、セグメントを意識せずに、以下のように表記することもできる。

Bスプライン関数も、バーンスタイン関数と同様に、次の性質を満たす。
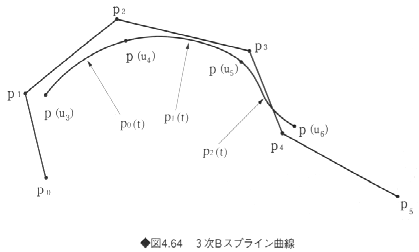
 ここで式(4.51)を式(4.42)と見比べると、Bスプライン曲線もベジェ曲線のように、点piの荷重平均の形式になっている。つまり、n次のBスプライン曲線の各セグメントは、通常(n+1)個の制御点によって定められる。この性質をBスプライン曲線の局所性とよぶ。また隣同士のセグメントはn個の制御点を共有しており、Bスプライン関数の性質から曲線もCn-1級の連続性を保証する。このほか、Bスプライン曲線には、ベジェ曲線と同様に、凸包性、変動減少性、直線再現性、アフィン不変性などの性質がある。図4.64に一様ノットの場合の3次Bスプライン曲線の例を示す。
ここで式(4.51)を式(4.42)と見比べると、Bスプライン曲線もベジェ曲線のように、点piの荷重平均の形式になっている。つまり、n次のBスプライン曲線の各セグメントは、通常(n+1)個の制御点によって定められる。この性質をBスプライン曲線の局所性とよぶ。また隣同士のセグメントはn個の制御点を共有しており、Bスプライン関数の性質から曲線もCn-1級の連続性を保証する。このほか、Bスプライン曲線には、ベジェ曲線と同様に、凸包性、変動減少性、直線再現性、アフィン不変性などの性質がある。図4.64に一様ノットの場合の3次Bスプライン曲線の例を示す。
《5》NURBS曲線
NURBS(非一様有理Bスプライン)曲線20)は、制御点piと各制御点に対応する重みwi、ノットベクトルtiによって定義した曲線である。NURBS曲線の重みは、有理ベジェ曲線の重みと同様に制御点を相対的に重みづけする値で、すべての重みが等しいとBスプライン曲線と等しくなる。L個のセグメントからなるn次のNURBS曲線は、パラメータ区間[tn,tn+L-1]において定義される区分有理式曲線であり、以下の式で与えられる。
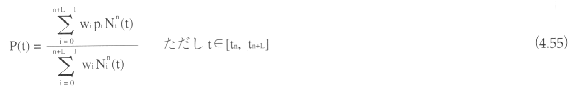
ここで、Nni(t)はn次Bスプライン関数である。NURBS曲線は有理ベジェ曲線とBスプライン曲線の性質をあわせもつ曲線である。
 2次曲面
2次曲面
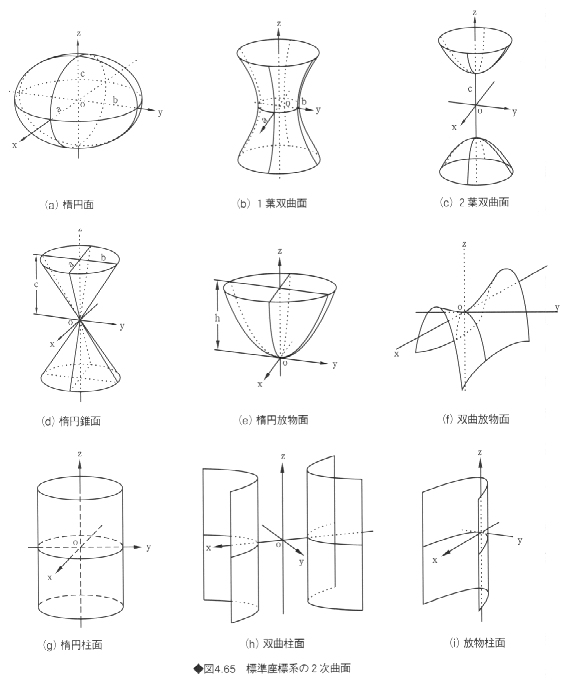
2次曲面23)は、2次多項式によって表現される代数曲面であり、以下の式によって表現される。
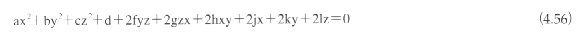
2次曲面がある1点に関して点対称であるとき、その点を2次曲面の中心とよぶ。中心をもつ2次曲面を有心であるといい、中心をもたない曲面を無心であるという。2次曲面は、楕円面(ellipsoid)、1葉双曲面(hyperboloid
of one sheet)、2葉双曲面(hyperboloid of two sheets)、楕円錐面(elliptic cone)、楕円放物面(elliptic
paraboloid)、双曲放物面(hyperbolic paraboloid)、楕円柱面(elliptic cylinder)、双曲柱面(hyperbolic
cylinder)、放物柱面(parabolic cylinder)に分類される。
このうち、楕円柱面、双曲柱面、放物柱面をまとめて2次柱面とよぶこともある。楕円面、1葉双曲面、2葉双曲面、楕円錐面、楕円柱面、双曲柱面は有心であり、楕円放物面、双曲放物面、放物柱面は無心である。
2次曲面は、平面上の平行移動と回転によって、図4.65に示す標準座標系に変換できる。標準座標系における2次曲面の表現式は以下のようになる。
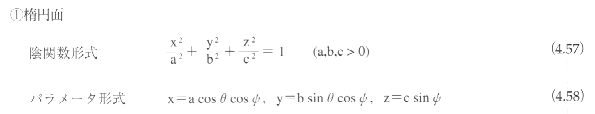
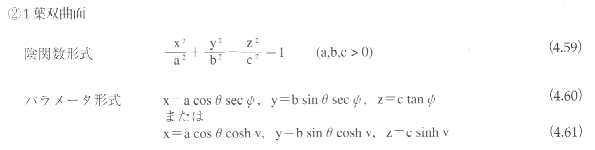
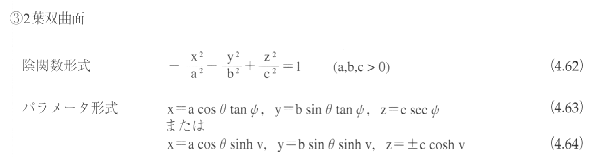
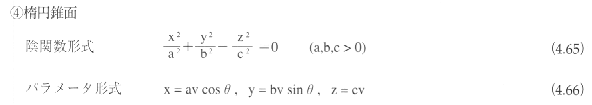
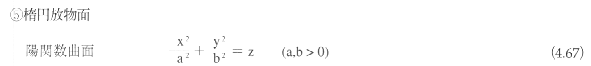
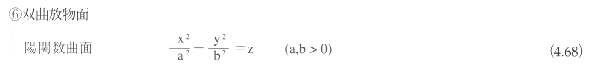
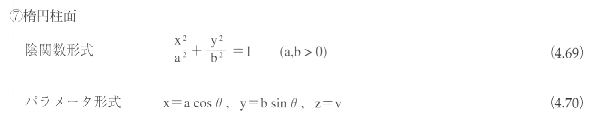
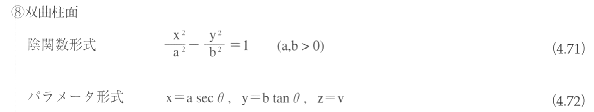
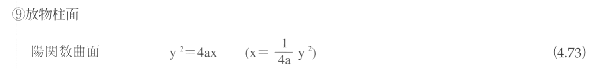
トーラス面
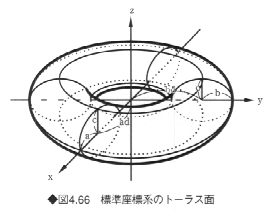
トーラス面は2次曲面ではないが、2次曲面を拡張したものと考えられる。トーラス面も、平面上の平行移動と回転によって、図4.66に示す標準座標系に変換できる。標準座標系におけるトーラス面の表現式は以下のようになる。
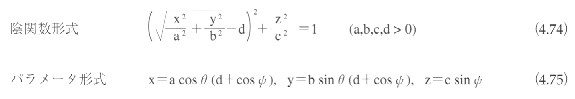
超2次曲面
超2次曲面(superquadrics)17)は、2次曲面を拡張して、丸みを制御できるようにしたものである。超2次曲面には、超楕円面(superellipsoid)、超1葉双曲面(superhyperboloid
of one sheet)、超2葉双曲面(superhyperboloid of two sheets)、超トーラス面(supertroid)などがある。
超2次曲面は、平面上の平行移動と回転によって、標準座標系に変換できる。標準座標系における超2次曲面の表現式は以下のようになる。
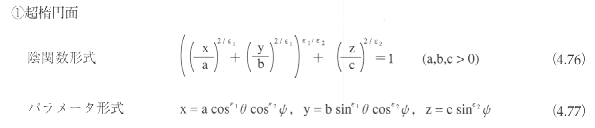
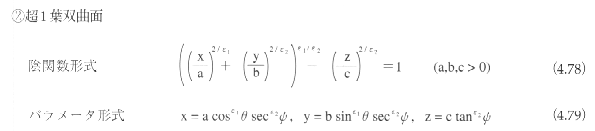
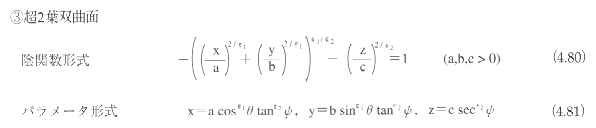
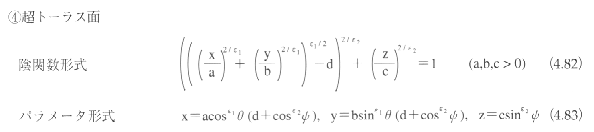
超2次曲面の例を図4.67に示す。

 パラメトリック曲面
パラメトリック曲面
パラメトリック曲面はパラメータの陽関数形式で表現された曲面である。このときの関数が多項式関数である場合には多項式曲面(polynomial surface)とよばれ、有理式関数である場合には有理式曲面ないし有理曲面(rational
surface)とよばれる。
パラメトリック曲面では、パラメトリック曲線と同様に、適当なパラメータ領域に対応する曲面の一部分のみを利用し、曲面全体を扱うことはない。この曲面の部分のことをパッチ(patch)とよぶ。複雑な曲面形状を扱う場合には、複数のパッチをつなぎ合わせて1枚の曲面を表現する。このように複数の曲面を合わせて1枚の曲面を表す手法を複合曲面(composite
surface)とよぶ。
CGでは、以下にあげる曲面がよく利用されている。
双3次曲面
ベジェ曲面
有理ベジェ曲面
Bスプライン曲面
NURBS曲面
クーンズ曲面はエルミート曲線を曲面に拡張したものである。ベジェ曲面、有理ベジェ曲面、Bスプライン曲面、NURBS曲面は、テンソル積曲面とよばれる曲面であり、それぞれベジェ曲線、有理ベジェ曲線、Bスプライン曲線、NURBS曲線を拡張したものである。
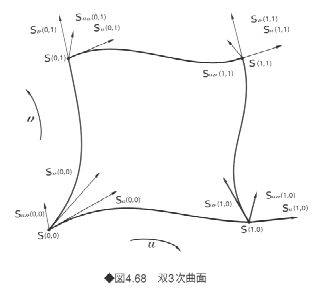
《1》双3次曲面
双3次曲面は、図4.68のように四辺形パッチの四隅の点とそこでの接ベクトルとツイストベクトルによって定義される3次の多項式曲面である。双3次曲面の定義されるパラメータ領域はu∈[0,1]、v∈[0,1]である。双3次曲面は3次エルミート関数を用いて、次のように表現される。
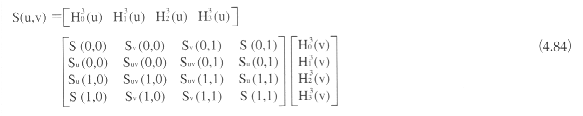
ここで、

である。つまり、Su(u,v)は(u,v)におけるu方向の接ベクトル、Sv(u,v)は(u,v)におけるv方向の接ベクトルを表す。またSuv(u,v)は(u,v)におけるツイストベクトルとよばれ、その位置での曲面のねじれ方を表す。
《2》ベジェ曲面
ベジェ曲面は格子状に並んだ制御点pijによって定義した曲面である。このとき制御点は曲面の四隅の点と概形を定める。ベジェ曲面も、u∈[0,1]、v∈[0,1]なるパラメータ領域において定義される多項式曲面である。uに関してn次、vに関してm次の式であれば、n×m次曲面とよばれ、(n+1)×(m+1)個の制御点によって表現される。n=mのときは双n次曲面とよばれる。ベジェ曲面は次式で与えられる。

ここで、Bni(u)、Bmj(v)は、それぞれn次とm次のバーンスタイン関数である。したがって、式(4.83)を見ると、ベジェ曲面上の点S(u,v)は、制御点pijの荷重平均になっており、パラメータu、vが変化すると、各制御点に対する重みBni(u)Bmj(v)が連続的に変化して、点S(u,v)が連続的に移動する。この点の軌跡がベジェ曲面となる。
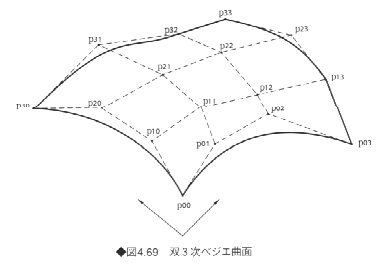
CGでは次数が3次までのベジェ曲面がよく用いられる。双3次ベジェ曲面は、図4,69に示すよう
に、16個の制御点p00、......、p33によって定められる。図でわかるように、ベジェ曲面の四隅の点は 制御点に一致し、四辺は3次のベジェ曲線になっている。とうぜん、四隅におけるu方向およびv方向の接ベクトルは、四隅の制御点と1つ隣の制御点を結んだ向きになる。この性質はベジェ曲線の端点一致性に対応する性質であり、ベジェ曲面がよく用いられる理由の1つとなっている。
ベジェ曲面の性質には、このほかに以下のものがある。
①凸包性
u∈[0,1]、v∈[0,1]における曲面は制御点の構成する凸包の内部に存在する。
②変動減少性
曲面は制御点配列の形状を滑らかにした形になる。
③疑似局所制御性
制御点を移動すると、その点に対応する曲面部分が大きく変形する。
④平面再現性
制御点を平面上に格子状に配すると曲面は平面になる。
⑤アフィン不変件
曲面にアフィン変換を施した結果とアフィン変換を施した制御点から得られる曲面が等しくなる。
CGの分野で、新しいレンダリングアルゴリズムを提案したり、アルゴリズムの速度を比較したりするとき、標準の物体としてしばしば使われたことで有名なティーポットは約40枚の双3次ベジェ曲面を接続した曲面として定義されている(図4.70)。
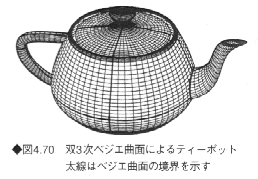
CGでお馴染みのティーポット
図4.70に示したティーポットには実物が存在する。
アメリカのユタ大学でCGを研究していたグループのメンバーがその実物のティーポットから座標を測定し、ベジェ曲面の制御点を定めた。実物は図4.70に比べると、もう少し背が高かったが、みばえを考慮して、計算により、背を低くした。このようなことが簡単にできるのが、コンピュータによるモデリングのよいところである。
なお、実物はボストンの計算機博物館(Computer Museum)に展示されている。
《3》有理ベジェ曲面
有理ベジェ曲面は、制御点pijと各制御点に対応する重みwijによって定義した曲面である。この重みは、有理ベジェ曲線と同様に、制御点を相対的に重みづけする値で、すべての重みが等しいとベジェ曲面と等しくなる。有理ベジェ曲面は、u∈[0,1]、v∈[0,1]なるパラメータ領域において定義される有理式曲面で、以下の式で与えられる。

ここでBni(t)はn次のバーンスタイン関数である。
有理ベジェ曲面はベジェ曲面の性質に加えて以下の性質をもっている。
①重み
重みwijによって曲面の形をより細かく制御できる。
②2次曲面
ベジェ曲面では表現できない2次曲面を正確に表現できる。
③射影不変件
曲面に射影変換を施した結果と射影変換を施した制御点から得られる曲面が等しくなる。
《4》Bスプライン曲面
Bスプライン曲面は、制御点pijとu方向とv方向のノット列(ノットベクトル)ui、vjによって定義された曲面である。L×K個のパッチからなるn×m次のBスプライン曲面はパラメータ区間u∈[un,un+L]、V∈[vm,vm+k]において定義される区分多項式曲面で、以下の式で与えられる。
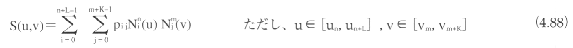
ここでNni(u)、Nmj(v)は、それぞれn次とm次のBスプライン関数である。なお、n=mのときにはベジェ曲面同様に、双n次のBスプライン曲面とよぶこともある。
n×m次のBスプライン曲面の各パッチは、通常(n+1)×(m+1)個の制御点によって定められる。この性質をBスプライン曲面の局所性とよぶ。また隣どうしのパッチはu方向でCn-1級の連続性を、v方向でCm-1級の連続性を保証する。このほか、Bスプライン曲面には、ベジェ曲面と同様に、凸包性、変動減少性、平面再現性、アフィン不変性などの性質がある。
《5》NURBS曲面
NURBS曲面20)は、制御点pijと各制御点に対応する重みwij、u方向とv方向のノット列(ノットベクトル)ui、vjによって定義した曲面である。NURBS曲面の重みは、有理ベジェ曲面の重みと同様に、制御点を相対的に重みづけする値で、すべての重みが等しいとBスプライン曲面と等しくなる。L×K個のパッチからなるn×m次のNURBS曲面は、パラメータ区間u∈[un,un+1]、v∈[vm,vm+k]において定義される区分有理式曲面であり、以下の式で与えられる。

ここでNni(u)、Nmj(v)は、それぞれn次とm次のBスプライン関数である。NURBS曲面は有理ベジェ曲面とBスプライン曲面の性質をあわせもつ。
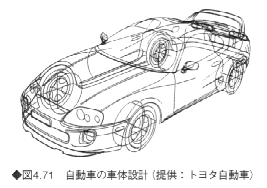
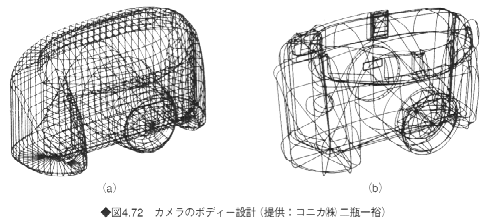
Bスプライン曲面やNURBS曲面は、自動車、航空機、家庭電器製品、カメラ、容器など、さまざまな工業製品の設計に広く使われている。図4.71に自動車の例を、図4.72にカメラの例を示す。
【参考文厭】
1)福永節夫:図学概説,培風館(1969).
2)日本図学会(編):図形科学ハンドブック,森北出版(1980)
3)Courbes Mathematics, Palais de la Decouverte(1976)
4)Hermann Von Baravalle : GEOMETRE/ALS SPRACHE DER FORMEN, Verlag Freies Geistesleben
Stuttgart(1963).
5)John Whitney : Digital Harmony,MaGraw-Hill(1980).
6)J.Bourgoin : Arabic Geometrical Pattern & Design, Dover Publication Inc.(1973).
7)Herman Weyl(遠山啓 訳) : シンメトリー,紀伊國屋書店(1970).
8)Douglas Davis : Art and Future, Praeger Publishers Inc.(1973).
9)Jasia Reichardt : Cybemetic Serendipity, Frederick A. Praeger Inc.(1969).
10)柳 亮:黄金分割,美術出版社(1965).
11)日本図学会(編):CGハンドブック,森北出版(1989).
12)Mgel V.Walters, John Bromham: Principle of Perspective, Architectual Press(1970).
13)William C.Seitz : The Responsive Eye, The Museum Modem Art (1965).
14)渕上季代絵 : フラクタルCGコレクション,サイエンス社(1987),
15)(財)画像情報教育振興協会 : Computer Graphics 教育者用教材パッケージ Version 1.Od(1994).
16)長島忍 : 形状モデルの生成と応用, PIXEL,99,pp.65-70(1990).
17)A.H.Barr : Superquadrrics and Angle-Preserving Transformations, IEEE CG&A,Vol.1,
No.1,pp,11-23(1981).
18)G.Farin : Curves and Suraces for Computer Aided Geometrlc Design, Third Edition,
Academic Press, p.473(1993).(翻訳)木村文彦監修,山口泰監訳 : CAGDのための曲線・曲面理論共立出版,p.330 (1991).
19)J.Hoschek, D.Lasser : Fundamentals of Computer Aided Geometric Design, A
K Peters, Ltd.,p.727 (1993).
20)L.Piegl : On NURBSA Survey, IEEE CG&A, Vol.11, NO.1, PP.55-71(1991),
21)鳥谷浩志,千代倉弘明(編著) : 3次元CADの基礎と応用,共立出版p.228(1991).
22)山口富士夫 : コンピュータディスプレイによる形状処理工学[I],[II],日刊工業新聞社,p.193,218(1982).
23)日本図学会(編) : CGハンドブック,森北出版,p.516(1989).



























































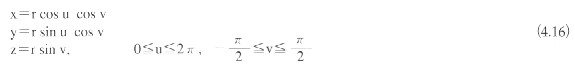



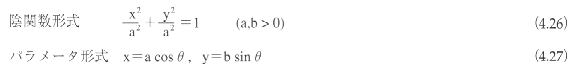
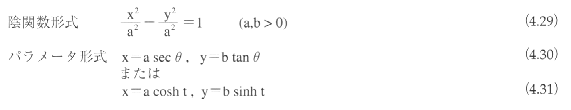
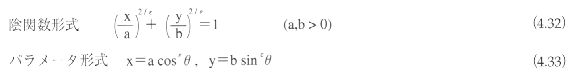
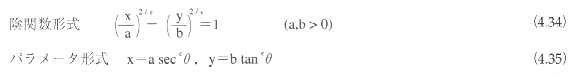



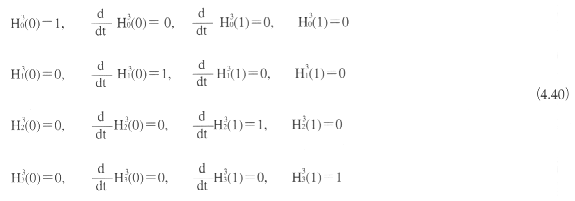







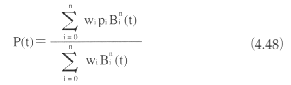

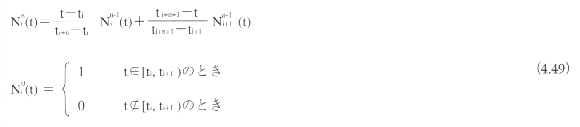





 ここで式(4.51)を式(4.42)と見比べると、Bスプライン曲線もベジェ曲線のように、点piの荷重平均の形式になっている。つまり、n次のBスプライン曲線の各セグメントは、通常(n+1)個の制御点によって定められる。この性質をBスプライン曲線の局所性とよぶ。また隣同士のセグメントはn個の制御点を共有しており、Bスプライン関数の性質から曲線もCn-1級の連続性を保証する。このほか、Bスプライン曲線には、ベジェ曲線と同様に、凸包性、変動減少性、直線再現性、アフィン不変性などの性質がある。図4.64に一様ノットの場合の3次Bスプライン曲線の例を示す。
ここで式(4.51)を式(4.42)と見比べると、Bスプライン曲線もベジェ曲線のように、点piの荷重平均の形式になっている。つまり、n次のBスプライン曲線の各セグメントは、通常(n+1)個の制御点によって定められる。この性質をBスプライン曲線の局所性とよぶ。また隣同士のセグメントはn個の制御点を共有しており、Bスプライン関数の性質から曲線もCn-1級の連続性を保証する。このほか、Bスプライン曲線には、ベジェ曲線と同様に、凸包性、変動減少性、直線再現性、アフィン不変性などの性質がある。図4.64に一様ノットの場合の3次Bスプライン曲線の例を示す。